Triangular Cupola Calculator
Calculator and formulas for a triangular cupola (Johnson solid J3)
Triangular Cupola Calculator
The Triangular Cupola
A triangular cupola has a hexagonal base and a triangular top (Johnson solid J₃).
Triangular Cupola Properties
Hexagon to triangle: Hexagonal base with triangular top
Triangular Cupola Structure
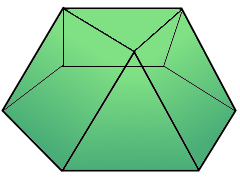
Hexagonal base with triangular top.
Johnson solid J₃.
|
|
What is a Triangular Cupola?
A triangular cupola is an elegant Johnson solid with unique geometry:
- Definition: Cupola with hexagonal base and triangular top
- Classification: Johnson solid J₃
- Base: Regular hexagon
- Top: Equilateral triangle
- Sides: 3 squares + 3 triangles
- Uniform edges: All edges equal length
Geometric Properties of the Triangular Cupola
The triangular cupola showcases remarkable geometric properties:
Basic Parameters
- Faces: 8 faces total (1+1+3+3)
- Edges: 15 edges (all equal)
- Vertices: 9 vertices
- Euler characteristic: V - E + F = 9 - 15 + 8 = 2
Special Properties
- Cupola structure: Hexagon-to-triangle transition
- Mixed faces: Hexagon, triangle, squares, triangles
- Johnson solid: Part of the J₃ family
- Uniform edges: All edges same length
Mathematical Relationships
The triangular cupola follows elegant mathematical principles:
Volume Formula
V = (5/6)√2 × a³ ≈ 1.1785 × a³. Elegant coefficient with √2.
Surface Formula
S = (a²/2)(6 + 5√3) ≈ 7.33 × a². Complex but elegant.
Applications of the Triangular Cupola
Triangular cupolas find applications in various fields:
Architecture & Construction
- Unique roof structures
- Modern architectural elements
- Decorative building features
- Skylight designs
Science & Technology
- Crystal structure analysis
- Molecular geometry models
- Engineering components
- 3D design applications
Education & Teaching
- Advanced geometry education
- Johnson solid studies
- 3D modeling exercises
- Mathematical demonstrations
Art & Design
- Sculptural works
- Architectural ornaments
- Decorative objects
- Geometric art pieces
Triangular Cupola Formulas
Volume (V)
Volume with elegant 5/6 × √2 coefficient
Surface Area (S)
Complex surface area with √3 factor
Height (h)
Height with √6/3 factor
Circumradius (r)
Simple circumradius equal to edge length
Triangular Cupola Parameters
Regular hexagon
Equilateral triangle
3 squares + 3 triangles
Johnson J₃
Elegant cupola connecting hexagon to triangle
Calculation Example for Triangular Cupola
Given
Find: All properties of the triangular cupola
1. Volume Calculation
For edge length a = 10:
\[V = \frac{5}{6} \cdot 1000 \cdot \sqrt{2}\] \[V = 833.33 \cdot 1.414\] \[V \approx 1178.5\]The volume is approximately 1178.5 cubic units
2. Surface Area Calculation
For edge length a = 10:
\[S = \frac{100}{2} \cdot (6 + 5\sqrt{3})\] \[S = 50 \cdot (6 + 8.66)\] \[S \approx 733\]The surface area is approximately 733 square units
3. Height Calculation
For edge length a = 10:
\[h = \frac{\sqrt{6}}{3} \cdot 10\] \[h \approx 0.8165 \cdot 10\] \[h \approx 8.17\]The height is approximately 8.17 length units
4. Circumradius Calculation
For edge length a = 10:
\[r = a = 10\]The circumradius is 10 length units
5. Complete Triangular Cupola
The elegant triangular cupola with perfect hexagon-to-triangle transition
The Triangular Cupola: Hexagonal to Triangular Elegance
The triangular cupola represents one of the most geometrically fascinating Johnson solids, demonstrating the elegant transition from a hexagonal base to a triangular top. As Johnson solid J₃, it showcases how different regular polygons can be connected through carefully arranged intermediate faces, creating a harmonious structure that bridges six-fold and three-fold symmetry. This unique geometric form has captured the attention of mathematicians, architects, and designers who appreciate its perfect balance of complexity and elegance.
The Art of Geometric Transition
The triangular cupola showcases the beauty of geometric interpolation:
- Hexagonal foundation: Regular hexagon provides stable six-sided base
- Triangular crown: Equilateral triangle creates elegant three-fold top
- Mixed transition: 3 squares and 3 triangles bridge different symmetries
- Uniform edges: All 15 edges have identical length
- Johnson classification: Distinguished J₃ designation
- Mathematical beauty: Formulas with √2, √3, and √6
- Symmetric elegance: Perfect balance of different face types
Mathematical and Structural Significance
Geometric Innovation
The triangular cupola demonstrates how hexagonal and triangular symmetries can be elegantly combined, creating a structure that maintains the benefits of both six-fold and three-fold rotational symmetry while bridging them seamlessly.
Mathematical Complexity
The formulas involving multiple square roots (√2, √3, √6) reflect the sophisticated mathematical relationships required to balance different polygonal symmetries in a single coherent structure.
Structural Versatility
The combination of different face types creates a structure with excellent load distribution properties, making it useful in architectural applications where both stability and aesthetic appeal are important.
Design Inspiration
The triangular cupola's unique ability to transition between different symmetries has inspired architects and designers to explore how different geometric forms can be harmoniously combined in practical applications.
Summary
The triangular cupola stands as a masterpiece of geometric transition, elegantly bridging the gap between hexagonal and triangular symmetries. As Johnson solid J₃, it demonstrates how mathematical precision can create forms that are both structurally sound and aesthetically pleasing. Its sophisticated formulas, involving multiple square roots, reflect the complex mathematical relationships necessary to balance different polygonal forms in perfect harmony. From its hexagonal foundation through its mixed square and triangular sides to its triangular crown, every aspect of this cupola speaks to the beauty of geometric interpolation. Whether studied for its mathematical properties, admired for its structural elegance, or applied in architectural and design contexts, the triangular cupola continues to inspire those who appreciate the subtle art of combining different geometric symmetries into a single, unified form.
|
|
|
|