Square Cupola Calculator
Calculator and formulas for a square cupola (Johnson solid J4)
Square Cupola Calculator
The Square Cupola
A square cupola has an octagonal base and a square top (Johnson solid J₄).
Square Cupola Properties
Mixed faces: Octagonal base, square top, square and triangular sides
Square Cupola Structure
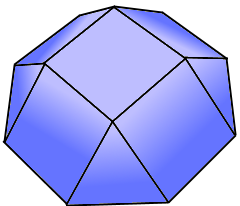
Octagonal base with square top.
Johnson solid J₄.
|
|
What is a Square Cupola?
A square cupola is one of the fundamental Johnson solids:
- Definition: Cupola with octagonal base and square top
- Classification: Johnson solid J₄
- Base: Regular octagon
- Top: Square
- Sides: 4 squares + 4 triangles
- Uniform edges: All edges equal length
Geometric Properties of the Square Cupola
The square cupola showcases remarkable geometric properties:
Basic Parameters
- Faces: 10 faces total (1+1+4+4)
- Edges: 20 edges (all equal)
- Vertices: 12 vertices
- Euler characteristic: V - E + F = 12 - 20 + 10 = 2
Special Properties
- Cupola structure: Truncated pyramid form
- Regular faces: All faces are regular polygons
- Johnson solid: Part of the J₄ family
- Uniform edges: All edges same length
Mathematical Relationships
The square cupola follows elegant mathematical principles:
Volume Formula
V = (1 + 2√2/3) × a³ ≈ 1.9428 × a³. Elegant root formula.
Surface Formula
S = (7 + 2√2 + √3) × a² ≈ 11.56 × a². Multiple root factors.
Applications of the Square Cupola
Square cupolas find applications in various fields:
Architecture & Construction
- Roof structures and cupolas
- Decorative building elements
- Modern architectural features
- Skylight constructions
Science & Technology
- Crystal structure analysis
- Molecular geometry models
- Engineering components
- 3D design applications
Education & Teaching
- Geometry education
- Johnson solid studies
- 3D modeling exercises
- Mathematical demonstrations
Art & Design
- Sculptural works
- Architectural ornaments
- Decorative objects
- Geometric patterns
Square Cupola Formulas
Volume (V)
Volume with elegant √2 coefficient
Surface Area (S)
Surface area with √2 and √3 factors
Height (h)
Height with simple √2/2 factor
Circumradius (r)
Complex circumradius with nested radicals
Square Cupola Parameters
Regular octagon
Square
4 squares + 4 triangles
Johnson J₄
Classic cupola structure connecting octagon to square
Calculation Example for Square Cupola
Given
Find: All properties of the square cupola
1. Volume Calculation
For edge length a = 10:
\[V = \left(1 + \frac{2\sqrt{2}}{3}\right) \cdot 1000\] \[V = (1 + 0.9428) \cdot 1000\] \[V \approx 1942.8\]The volume is approximately 1942.8 cubic units
2. Surface Area Calculation
For edge length a = 10:
\[S = (7 + 2\sqrt{2} + \sqrt{3}) \cdot 100\] \[S = (7 + 2.828 + 1.732) \cdot 100\] \[S \approx 1156\]The surface area is approximately 1156 square units
3. Height Calculation
For edge length a = 10:
\[h = \frac{\sqrt{2}}{2} \cdot 10\] \[h \approx 0.7071 \cdot 10\] \[h \approx 7.07\]The height is approximately 7.07 length units
4. Circumradius Calculation
For edge length a = 10:
\[r = \frac{1}{2}\sqrt{5 + 2\sqrt{2}} \cdot 10\] \[r \approx 1.399 \cdot 10\] \[r \approx 13.99\]The circumradius is approximately 13.99 length units
5. Complete Square Cupola
The elegant square cupola with perfect octagonal-to-square transition
The Square Cupola: Octagonal Elegance
The square cupola represents one of the most architecturally significant Johnson solids, embodying the elegant transition from an octagonal base to a square top. As Johnson solid J₄, it showcases the beauty of geometric interpolation - how a regular octagon can smoothly connect to a square through a combination of square and triangular faces. This cupola structure has inspired architects and designers for centuries, appearing in everything from classical building cupolas to modern architectural elements.
The Beauty of Cupola Architecture
The square cupola showcases the perfection of architectural geometry:
- Octagonal foundation: Regular octagon provides stable base
- Square crown: Perfect square top creates elegant completion
- Mixed sides: 4 squares and 4 triangles form smooth transition
- Uniform edges: All 20 edges have identical length
- Johnson classification: Prestigious J₄ designation
- Architectural heritage: Classic cupola design principle
- Mathematical elegance: Beautiful formulas with √2 and √3
Mathematical and Architectural Significance
Geometric Transition
The square cupola demonstrates how different regular polygons can be elegantly connected through intermediate faces, creating a smooth geometric transition that is both mathematically precise and visually pleasing.
Architectural Heritage
This form has been used in architecture for millennia, from ancient temples to modern buildings, proving its timeless appeal and structural efficiency in creating elevated spaces and decorative elements.
Mathematical Beauty
The formulas involving √2 and √3 reflect the deep mathematical relationships between the octagonal base, square top, and triangular transition faces, showcasing the elegant interplay of different geometric forms.
Structural Excellence
The cupola's tapered form provides excellent structural properties, efficiently distributing loads while creating visually striking silhouettes that enhance both function and aesthetics.
Summary
The square cupola stands as a perfect example of how mathematical precision can create architecturally significant forms. As Johnson solid J₄, it bridges the gap between pure geometry and practical application, demonstrating how an octagonal base can elegantly transition to a square top through carefully arranged square and triangular faces. Its mathematical properties, expressed through formulas involving √2 and √3, reflect the deep geometric relationships that make this form both structurally sound and aesthetically pleasing. Whether crowning a classical building, serving as a decorative element, or inspiring modern architectural design, the square cupola continues to exemplify the timeless appeal of geometric perfection in both mathematical theory and practical application.
|
|
|
|