Gyrobifastigium Calculator
Calculator and formulas for a gyrobifastigium (Johnson solid J26)
Gyrobifastigium Calculator
The Gyrobifastigium
The gyrobifastigium is a Johnson solid with four squares and four triangles (J26).
Gyrobifastigium Properties
The twisted double wedge: Four squares and four equilateral triangles
Gyrobifastigium Structure
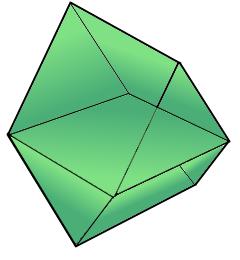
The twisted double wedge structure.
Four squares and four triangles.
|
|
What is a Gyrobifastigium?
A gyrobifastigium is a fascinating Johnson solid:
- Definition: Johnson solid J26
- Faces: 4 squares + 4 equilateral triangles
- All edges: Same length
- Vertices: 8 vertices total
- Edges: 14 edges
- Shape: Twisted double wedge
Geometric Properties of the Gyrobifastigium
The gyrobifastigium shows remarkable geometric properties:
Basic Parameters
- Square faces: 4 congruent squares
- Triangular faces: 4 equilateral triangles
- Euler characteristic: V - E + F = 8 - 14 + 8 = 2
- Edge uniformity: All edges equal length
Special Properties
- Johnson solid: One of the 92 Johnson solids
- Convex polyhedron: All faces convex
- Regular faces: Squares and equilateral triangles
- Twisted structure: Double wedge formation
Mathematical Relationships
The gyrobifastigium follows elegant mathematical laws:
Volume Formula
Simple and elegant formula. Volume proportional to a³.
Surface Area Formula
Combines square and triangle areas. Elegant geometric relationship.
Applications of the Gyrobifastigium
Gyrobifastigiums find applications in various fields:
Architecture & Engineering
- Structural elements
- Modern building designs
- Space-filling structures
- Architectural features
Science & Technology
- Crystallographic structures
- Molecular geometry
- Materials science
- Geometric modeling
Education & Teaching
- Geometry lessons
- Mathematical demonstrations
- 3D geometry studies
- Polyhedron exploration
Art & Design
- Sculptural works
- Art installations
- Decorative objects
- Geometric patterns
Gyrobifastigium Formulas
Volume (V)
Simple volume formula with √3
Surface Area (S)
Combined squares and triangles area
Height (h)
Height proportional to edge length
Edge Length (a)
Uniform edge length property
Gyrobifastigium Parameters
4 squares
4 equilateral triangles
8 vertices
14 edges
All properties based on equal edge length a
Calculation Example for a Gyrobifastigium
Given
Find: All properties of the gyrobifastigium
1. Volume Calculation
For a=10:
\[V = \frac{\sqrt{3}}{2} \cdot 10^3\] \[V ≈ 0.866 \cdot 1000\] \[V ≈ 866\]The volume is approximately 866 cubic units
2. Surface Area Calculation
For a=10:
\[S = (4 + \sqrt{3}) \cdot 10^2\] \[S ≈ (4 + 1.732) \cdot 100\] \[S ≈ 573.2\]The surface area is approximately 573.2 square units
3. Complete Gyrobifastigium
The gyrobifastigium with perfect geometric harmony
The Gyrobifastigium: The Twisted Double Wedge
The gyrobifastigium is one of the most elegant Johnson solids, representing the perfect harmony between squares and equilateral triangles. As Johnson solid J26, it demonstrates how regular faces can combine to create a convex polyhedron with remarkable symmetry and beauty. The mathematical elegance lies in the simple formulas that govern its geometry, making it both accessible to students and fascinating to researchers.
The Geometry of Perfection
The gyrobifastigium showcases the beauty of geometric harmony:
- Face uniformity: Only regular squares and equilateral triangles
- Edge equality: All 14 edges have identical length
- Convexity: All faces point outward
- Symmetry: Multiple axes of symmetry
- Johnson classification: One of exactly 92 Johnson solids
- Mathematical elegance: Simple √3-based formulas
- Construction: Can be built from simple components
Mathematical Beauty
Formula Simplicity
The gyrobifastigium's formulas are remarkably simple, involving only basic arithmetic operations with √3, making calculations straightforward and elegant.
Geometric Harmony
The combination of 4 squares and 4 triangles creates a perfect balance that results in a stable, aesthetically pleasing three-dimensional form.
Structural Integrity
The alternating arrangement of squares and triangles provides excellent structural properties, making it useful in engineering and architectural applications.
Educational Value
As one of the simpler Johnson solids, the gyrobifastigium serves as an excellent introduction to polyhedron geometry and spatial reasoning.
Summary
The gyrobifastigium represents the perfect marriage of simplicity and elegance in three-dimensional geometry. As Johnson solid J26, it demonstrates how regular faces can combine to create remarkable beauty and functionality. From its simple √3-based formulas to its practical applications in architecture and design, the gyrobifastigium continues to fascinate mathematicians, engineers, and artists alike. Its role as a bridge between basic geometric shapes and complex polyhedra makes it an invaluable tool for education and a source of inspiration for creative applications. Whether studied for its mathematical properties or admired for its aesthetic qualities, the gyrobifastigium stands as a testament to the enduring beauty of geometric form.
|
|
|
|