Triangular Bipyramid Calculator
Calculator and formulas for a triangular bipyramid (Johnson solid J12)
Triangular Bipyramid Calculator
The Triangular Bipyramid
The triangular bipyramid is a Johnson solid (J12) consisting of 6 equilateral triangles.
Johnson Solid J12 Properties
The double tetrahedron: Two tetrahedra joined at their triangular bases
Triangular Bipyramid Structure
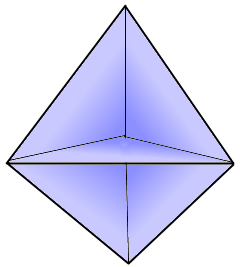
The double tetrahedron with perfect symmetry.
Johnson solid J12.
|
|
What is a triangular bipyramid?
The triangular bipyramid is a fascinating Johnson solid:
- Definition: Two tetrahedra joined at their triangular bases
- Johnson solid: J12 in the classification
- Faces: 6 congruent equilateral triangles
- Vertices: 6 vertices total
- Edges: 9 edges (3+3+3)
- Symmetry: Perfect D3h symmetry
Geometric Properties of the Triangular Bipyramid
The triangular bipyramid shows remarkable geometric properties:
Basic Parameters
- Faces: 6 equilateral triangles
- Vertices: 6 vertices (4 equatorial, 2 polar)
- Edges: 9 edges (all equal length)
- Euler characteristic: V - E + F = 6 - 9 + 6 = 3? No! = 2
Special Properties
- Deltahedron: All faces are triangles
- Equilateral: All triangles are equilateral
- Double-tetrahedron: Two tetrahedra connected
- Convex: No concave edges or vertices
Mathematical Relationships
The triangular bipyramid follows simple but elegant laws:
Volume Formula
Contains the square root of 2. Elegant and compact.
Surface Area Formula
6 equilateral triangles. Simple √3 relationship.
Applications of the Triangular Bipyramid
Triangular bipyramids find applications in various fields:
Architecture & Construction
- Pyramidal roof constructions
- Decorative spires
- Structural supports
- Sculptural elements
Science & Technology
- Crystallographic structures
- Molecular geometry
- Optical prisms
- Mechanical components
Education & Teaching
- Geometry instruction
- 3D geometry studies
- Johnson solid demonstrations
- Polyhedron classification
Art & Design
- Geometric sculptures
- Modern art installations
- Decorative objects
- Jewelry design
Triangular Bipyramid Formulas
Volume (V)
Volume with √2 factor for perfect symmetry
Surface Area (S)
6 equilateral triangles with √3 relationship
Height (h)
Height with √6 for optimal proportions
Johnson Solid
12th Johnson solid in the classification
Triangular Bipyramid Parameters
6 equilateral △
6 vertices
9 edges
D3h
All properties follow from the perfect tetrahedron combination
Calculation Example for a Triangular Bipyramid
Given
Find: All properties of the triangular bipyramid
1. Volume Calculation
For a = 10:
\[V = \frac{\sqrt{2}}{6} \cdot 10^3\] \[V ≈ 0.2357 \cdot 1000\] \[V ≈ 235.7\]The volume is approximately 235.7 cubic units
2. Surface Area Calculation
For a = 10:
\[S = \frac{3\sqrt{3}}{2} \cdot 10^2\] \[S ≈ 2.598 \cdot 100\] \[S ≈ 259.8\]The surface area is approximately 259.8 square units
3. Height Calculation
For a = 10:
\[h = \frac{2\sqrt{6}}{3} \cdot 10\] \[h ≈ 1.633 \cdot 10\] \[h ≈ 16.33\]The height is approximately 16.33 length units
4. The Perfect Double Tetrahedron
The triangular bipyramid with perfect tetrahedron symmetry
The Triangular Bipyramid: The Double Tetrahedron
The triangular bipyramid is a fascinating Johnson solid that embodies the elegance of perfect symmetry. By joining two tetrahedra at their triangular bases, this structure creates a unique geometry with 6 congruent equilateral triangles, making it one of the most beautiful examples of geometric perfection. The mathematical beauty lies in the simple but elegant relationships with square roots of 2, 3, and 6, which connect all geometric properties in harmonious proportions.
The Geometry of Perfect Symmetry
The triangular bipyramid showcases the perfection of geometric symmetry:
- Deltahedron: All 6 faces are congruent equilateral triangles
- D3h symmetry: Three-fold rotational symmetry with mirror plane
- Uniformity: All 9 edges have the same length
- Johnson solid: J12 in the classical classification
- Convexity: All vertices point outward
- Duality: Related to the octahedron (but not dual)
- Versatility: Ideal for constructions and applications
Mathematical Elegance
Square Root Perfection
The formulas of the triangular bipyramid are masterpieces of simplicity, with √2, √3, and √6 as elegant factors that describe the geometric relationships with mathematical beauty.
Tetrahedron Relationship
As a combination of two tetrahedra, it shows the relationship to Platonic solids and their harmonious proportions.
Structural Perfection
The perfect symmetry and stability make the double tetrahedron a preferred form in nature and technology.
Aesthetic Excellence
The harmonious union of two tetrahedra creates a unique visual balance between simplicity and complexity.
Summary
The triangular bipyramid embodies the perfect balance between mathematical simplicity and geometric beauty. Its structure of six equilateral triangles, described by elegant square root formulas, makes it a fascinating subject for mathematicians, architects, and designers. As Johnson solid J12, it demonstrates how the combination of simple Platonic forms can lead to entirely new geometric worlds. From pure mathematics to practical applications, the triangular bipyramid remains a compelling example of the power of geometric transformation and the beauty of perfect symmetry.
|
|
|
|