Rotunda Calculator
Calculator and formulas for a rotunda (Johnson solid J6)
Rotunda Calculator
The Rotunda (J6)
A rotunda is a Johnson solid with a decagonal base and pentagonal top.
Rotunda Properties
Johnson solid J6: Decagonal base with pentagonal top
Rotunda Structure
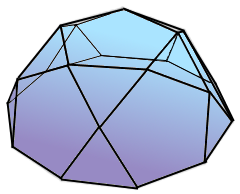
Johnson solid J6 with decagonal base.
Perfect union of pentagon and decagon.
|
|
What is a Rotunda?
A rotunda is one of the fascinating Johnson solids:
- Definition: Johnson solid J6
- Base: Regular decagon (10-sided)
- Top: Regular pentagon (5-sided)
- Side faces: 10 equilateral triangles + 5 squares
- Edges: All edges have equal length
- Symmetry: 5-fold rotational symmetry
Geometric Properties of the Rotunda
The rotunda demonstrates remarkable geometric properties:
Basic Structure
- Base: Regular decagon
- Top: Regular pentagon
- Transition: Via triangles and squares
- Johnson solid: J6
Special Properties
- Equal edges: All edges same length
- Regular faces: All faces are regular polygons
- Convex: No indentations
- Archimedean: Vertex-transitive structure
Mathematical Relationships
The rotunda follows elegant mathematical laws:
Volume Formula
Involves √5 and the golden ratio. Beautiful mathematical harmony.
Surface Formula
Combines pentagon and decagon areas. Elegant radical expressions.
Applications of the Rotunda
Rotundas find application in various fields:
Architecture & Construction
- Dome structures
- Rotunda buildings
- Garden pavilions
- Decorative elements
Science & Engineering
- Crystallographic studies
- Molecular geometry
- Structural analysis
- Material science
Education & Teaching
- Geometry education
- 3D modeling studies
- Johnson solid research
- Mathematical demonstrations
Art & Design
- Sculptural works
- Art installations
- Decorative objects
- Geometric patterns
Rotunda Formulas
Volume (V)
Volume with golden ratio √5
Surface Area (S)
Complex radical surface formula
Height (h)
Height with golden ratio relationships
Circumradius (r)
The golden ratio φ = (1+√5)/2
Rotunda Components
Regular decagon
Regular pentagon
10 triangles + 5 squares
All equal length
The rotunda bridges pentagon and decagon through perfect geometric relationships
Calculation Example for a Rotunda
Given
Find: All properties of the rotunda
1. Volume Calculation
For a = 10:
\[V = \frac{1}{12} \cdot (45 + 17\sqrt{5}) \cdot 1000\] \[V ≈ \frac{1}{12} \cdot (45 + 38.01) \cdot 1000\] \[V ≈ 6918\]The volume is approximately 6918 cubic units
2. Surface Area Calculation
For a = 10:
\[S ≈ 22.347 \cdot 100\] \[S ≈ 2235\]The surface area is approximately 2235 square units
3. Height Calculation
For a = 10:
\[h = \sqrt{1 + \frac{2}{\sqrt{5}}} \cdot 10\] \[h ≈ 1.376 \cdot 10\] \[h ≈ 13.76\]The height is approximately 13.76 units
4. Circumradius Calculation
For a = 10:
\[r = \frac{1 + \sqrt{5}}{2} \cdot 10\] \[r ≈ 1.618 \cdot 10\] \[r ≈ 16.18\]The circumradius is the golden ratio times the edge length
Complete Rotunda Solution
The rotunda showcases the beautiful relationship between pentagon and decagon
The Rotunda: Pentagon meets Decagon
The rotunda represents one of the most elegant examples of how geometric harmony can bridge different polygonal forms. As Johnson solid J6, it demonstrates the perfect mathematical relationship between the pentagon (5-fold symmetry) and the decagon (10-fold symmetry). The rotunda's structure, with its equal-length edges connecting these two fundamental shapes through triangles and squares, showcases the deep connections inherent in polyhedral geometry and the golden ratio's ubiquitous presence in natural mathematical relationships.
The Geometry of Perfect Union
The rotunda exemplifies the marriage of pentagon and decagon:
- Golden ratio presence: φ = (1+√5)/2 appears in multiple formulas
- Perfect symmetry: 5-fold rotational symmetry throughout
- Edge uniformity: All 25 edges have identical length
- Face regularity: All faces are regular polygons
- Convex structure: No concave indentations
- Johnson classification: One of exactly 92 Johnson solids
- Transition elegance: Smooth transition via triangles and squares
Mathematical Elegance
Golden Ratio Connections
The rotunda's formulas are deeply connected to the golden ratio φ, revealing the underlying mathematical harmony that connects pentagon-based and decagon-based geometries through radical expressions involving √5.
Polyhedral Perfection
As a Johnson solid, the rotunda satisfies strict criteria: all faces must be regular polygons, and the solid must be strictly convex. This makes it one of only 92 such perfect polyhedra.
Structural Harmony
The rotunda achieves perfect structural balance by connecting a 10-sided base to a 5-sided top through precisely arranged triangular and square faces, creating optimal stress distribution.
Aesthetic Appeal
The rotunda's combination of different regular polygons creates a visually striking form that has inspired architects, artists, and designers throughout history.
Summary
The rotunda stands as a testament to the power of geometric relationships and the ubiquity of the golden ratio in nature and mathematics. Its elegant structure, bridging the 5-fold symmetry of the pentagon with the 10-fold symmetry of the decagon, demonstrates how mathematical beauty emerges from the perfect balance of form and proportion. From its role as Johnson solid J6 to its applications in architecture and crystallography, the rotunda continues to fascinate mathematicians, scientists, and artists alike. Its formulas, rich with radical expressions and golden ratio relationships, reveal the deep mathematical truths that govern the harmony of three-dimensional space. As both a theoretical marvel and a practical form, the rotunda exemplifies the timeless beauty of mathematical perfection.
|
|
|
|