Pentagonal Pyramid Calculator
Calculator and formulas for a pentagonal pyramid (Johnson solid J2)
Pentagonal Pyramid Calculator
The Pentagonal Pyramid
The pentagonal pyramid is a Johnson solid with a pentagon base and 5 triangular faces (J2).
Pentagonal Pyramid Properties
The classic pyramid: Pentagon base with 5 equilateral triangular faces
Pyramid Structure
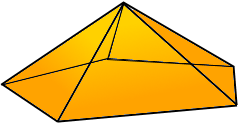
The classic pyramid structure.
Pentagon base with triangular sides.
|
|
What is a Pentagonal Pyramid?
A pentagonal pyramid is a fundamental Johnson solid:
- Definition: Johnson solid J2
- Base: Regular pentagon
- Sides: 5 equilateral triangles
- Vertices: 6 vertices total
- Edges: 10 edges
- All edges: Same length
Geometric Properties of the Pentagonal Pyramid
The pentagonal pyramid shows remarkable geometric properties:
Basic Parameters
- Pentagon base: Regular 5-sided polygon
- Triangular faces: 5 equilateral triangles
- Apex vertex: Single top vertex
- Edge uniformity: All edges equal length
Special Properties
- Johnson solid: One of the 92 Johnson solids
- Convex polyhedron: All faces convex
- Pyramidal structure: Classic pyramid form
- Golden ratio: Pentagon involves φ
Mathematical Relationships
The pentagonal pyramid follows elegant mathematical laws:
Volume Formula
Formula with (5+√5). Volume ≈ 0.3015 · a³.
Surface Area Formula
Advanced formula with √5. Surface ≈ 3.8855 · a².
Applications of the Pentagonal Pyramid
Pentagonal pyramids find applications in various fields:
Architecture & Engineering
- Pyramid structures
- Roof elements
- Decorative spires
- Monument designs
Science & Technology
- Crystal formations
- Molecular structures
- Optical pyramids
- Materials research
Education & Teaching
- Basic geometry education
- Pyramid volume studies
- Golden ratio exploration
- 3D modeling basics
Art & Design
- Sculptural works
- Geometric art
- Architectural models
- 3D printed objects
Pentagonal Pyramid Formulas
Volume (V)
Formula involving the golden ratio
Surface Area (S)
Complex formula with nested radicals
Height (h)
Height formula with golden ratio
Edge Length (a)
Uniform edge length property
Pentagonal Pyramid Parameters
Regular pentagon
5 equilateral triangles
6 vertices
10 equal edges
All properties based on equal edge length a
Calculation Example for a Pentagonal Pyramid
Given
Find: All properties of the pentagonal pyramid
1. Volume Calculation
For a=10:
\[V = \frac{5 + \sqrt{5}}{24} \cdot 1000\] \[V ≈ \frac{5 + 2.236}{24} \cdot 1000\] \[V ≈ 301.5\]The volume is approximately 301.5 cubic units
2. Height Calculation
For a=10:
\[h = \frac{5 - \sqrt{5}}{10} \cdot 10\] \[h ≈ \frac{5 - 2.236}{10} \cdot 10\] \[h ≈ 2.764\]The height is approximately 2.764 units
3. Complete Pentagonal Pyramid
The pentagonal pyramid with perfect golden ratio proportions
The Pentagonal Pyramid: Foundation of Golden Geometry
The pentagonal pyramid stands as one of the most fundamental and elegant Johnson solids, representing the perfect marriage of pyramidal geometry and pentagonal symmetry. As J2, it serves as an introduction to the fascinating world of Johnson solids while showcasing the mathematical beauty of the golden ratio. The formulas governing this polyhedron are deeply rooted in √5, the mathematical foundation of φ (phi), making it an excellent bridge between elementary geometry and advanced mathematical concepts.
The Pyramid of Golden Proportions
The pentagonal pyramid showcases fundamental geometric principles:
- Pentagonal base: Regular five-sided polygon with golden ratio properties
- Triangular faces: Five congruent equilateral triangles
- Edge uniformity: All 10 edges have identical length
- Golden ratio formulas: Volume and height involve √5
- Pyramidal elegance: Classic pyramid form with pentagonal twist
- Structural simplicity: One of the simpler Johnson solids
- Educational value: Perfect introduction to advanced polyhedra
Mathematical Foundation and Beauty
Golden Ratio Connection
The pentagonal pyramid's formulas beautifully demonstrate how the golden ratio emerges naturally in three-dimensional geometry, creating harmonious mathematical relationships.
Geometric Simplicity
Despite involving complex mathematical constants, the pyramid maintains an elegant simplicity that makes it accessible to students while remaining fascinating to researchers.
Structural Foundation
The pyramidal form provides exceptional stability and has been used in architecture for millennia, from ancient pyramids to modern structural elements.
Educational Bridge
As one of the simpler Johnson solids, it serves as an excellent introduction to advanced polyhedron theory while maintaining mathematical rigor.
Summary
The pentagonal pyramid represents the perfect introduction to the world of Johnson solids, combining the familiar pyramidal form with the sophisticated mathematics of pentagonal geometry. As J2, it demonstrates how simple geometric concepts can lead to profound mathematical insights, particularly in the realm of the golden ratio. From its elegant √5-based formulas to its practical applications in architecture and design, the pentagonal pyramid continues to serve as both a teaching tool and a source of mathematical inspiration. Its role as a bridge between elementary geometry and advanced polyhedron theory makes it invaluable for education, while its structural properties ensure continued relevance in engineering and architectural applications. Whether studied for its mathematical elegance or admired for its geometric beauty, the pentagonal pyramid stands as a testament to the power of combining simplicity with sophistication in geometric form.
|
|
|
|