Snub Disphenoid Calculator
Calculator and formulas for a snub disphenoid (Johnson solid J84)
Snub Disphenoid Calculator
The Snub Disphenoid
A snub disphenoid is bounded by 12 equilateral triangles forming a twisted deltahedron (Johnson solid J₈₄).
Snub Disphenoid Properties
Pure triangular faces: 12 equilateral triangles only
Snub Disphenoid Structure
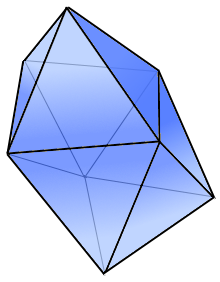
A deltahedron with 12 equilateral triangles.
Johnson solid J₈₄.
|
|
What is a Snub Disphenoid?
A snub disphenoid is one of the most elegant Johnson solids:
- Definition: Pure deltahedron with 12 triangular faces
- Classification: Johnson solid J₈₄
- Faces: 12 congruent equilateral triangles
- Vertices: 8 vertices total
- Edges: 18 edges (all equal length)
- Symmetry: D₂ₐ dihedral symmetry
Geometric Properties of the Snub Disphenoid
The snub disphenoid showcases remarkable geometric properties:
Basic Parameters
- Faces: 12 equilateral triangles
- Edges: 18 edges (all equal)
- Vertices: 8 vertices
- Euler characteristic: V - E + F = 8 - 18 + 12 = 2
Special Properties
- Deltahedron: All faces are triangles
- Convex: All vertices point outward
- Johnson solid: Part of the J₈₄ family
- Uniform edges: All edges same length
Mathematical Relationships
The snub disphenoid follows elegant mathematical principles:
Volume Formula
V ≈ 0.8595 × a³ for edge length a. Derived from triangular geometry.
Surface Formula
S = 3√3 × a² for 12 triangles. Simple and elegant.
Applications of the Snub Disphenoid
Snub disphenoids find applications in various fields:
Architecture & Construction
- Geodesic dome components
- Modern building elements
- Structural frameworks
- Decorative features
Science & Technology
- Crystallographic studies
- Molecular modeling
- Materials science
- 3D printing designs
Education & Teaching
- Geometry education
- 3D visualization
- Mathematical modeling
- Johnson solid studies
Art & Design
- Sculptural works
- Geometric art
- Jewelry design
- Architectural details
Snub Disphenoid Formulas
Surface Area (S)
Surface area with √3 factor for 12 triangles
Volume (V)
Approximate volume coefficient for snub disphenoid
Snub Disphenoid Parameters
12 equilateral triangles
18 equal edges
8 vertices
Johnson J₈₄
Pure deltahedron with only triangular faces
Calculation Example for Snub Disphenoid
Given
Find: All properties of the snub disphenoid
1. Surface Area Calculation
For edge length a = 10:
\[S = 3\sqrt{3} \cdot 10^2\] \[S = 3\sqrt{3} \cdot 100\] \[S \approx 5.196 \cdot 100 = 519.6\]The surface area is approximately 519.6 square units
2. Volume Calculation
For edge length a = 10:
\[V \approx 0.8595 \cdot 10^3\] \[V \approx 0.8595 \cdot 1000\] \[V \approx 859.5\]The volume is approximately 859.5 cubic units
3. Complete Snub Disphenoid
The elegant snub disphenoid with perfect triangular symmetry
The Snub Disphenoid: Triangular Perfection
The snub disphenoid represents one of the most elegant examples of geometric perfection in the Johnson solid family. As Johnson solid J₈₄, it showcases the beauty of pure triangular geometry - every face is an equilateral triangle, creating a harmonious deltahedron that embodies mathematical elegance. Its unique structure demonstrates how simple geometric principles can create complex and beautiful three-dimensional forms.
The Beauty of Triangular Geometry
The snub disphenoid showcases the perfection of triangular construction:
- Pure deltahedron: All 12 faces are equilateral triangles
- Uniform edges: All 18 edges have identical length
- Convex form: All vertices point outward uniformly
- Johnson classification: Member of the prestigious J₈₄ family
- Triangular perfection: No other face types needed
- Mathematical elegance: Simple yet sophisticated geometry
- Structural integrity: Triangles provide maximum stability
Mathematical Elegance
Geometric Perfection
The snub disphenoid demonstrates how equilateral triangles can be arranged to create a closed, convex polyhedron with remarkable symmetry and aesthetic appeal.
Structural Excellence
The triangular faces provide inherent structural strength, making the snub disphenoid an ideal shape for architectural and engineering applications.
Mathematical Simplicity
Despite its complex appearance, the formulas for surface area and volume are surprisingly elegant, involving simple coefficients and the fundamental √3 factor.
Visual Harmony
The arrangement of 12 triangular faces creates a visually pleasing form that balances complexity with symmetry, making it popular in art and design.
Summary
The snub disphenoid stands as a testament to the beauty of pure geometric form. As Johnson solid J₈₄, it represents the pinnacle of triangular construction - twelve equilateral triangles arranged in perfect harmony to create a convex deltahedron of exceptional elegance. Its mathematical properties, from the simple surface area formula involving √3 to the precise volume coefficient, demonstrate how geometric perfection can be expressed through elegant mathematical relationships. Whether studied for its geometric properties, admired for its visual appeal, or applied in practical design, the snub disphenoid continues to fascinate mathematicians, architects, and artists alike with its perfect balance of simplicity and sophistication.
|
|
|
|