Regelmäßiges Fünfeck (Pentagon) berechnen
Rechner und Formeln für regelmäßige Fünfecke
Pentagon Rechner
Regelmäßiges Fünfeck
Ein regelmäßiges Pentagon hat 5 gleich lange Seiten und 5 gleich große Winkel (108°). Eng verbunden mit der goldenen Zahl φ.
Regelmäßiges Pentagon
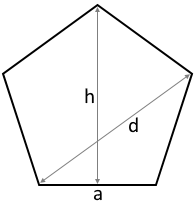
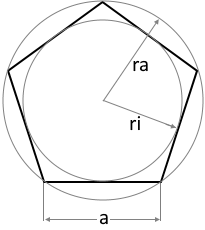
Die Diagramme zeigen ein regelmäßiges Fünfeck mit allen relevanten Parametern.
Alle 5 Seiten sind gleich lang, alle Innenwinkel betragen 108°.
|
|
Eigenschaften eines regelmäßigen Fünfecks
Ein regelmäßiges Fünfeck (Pentagon) ist eine der mathematisch faszinierendsten geometrischen Formen:
- 5 gleiche Seiten: Alle Seitenlängen sind identisch
- 5 gleiche Winkel: Jeder Innenwinkel beträgt exakt 108°
- Winkelsumme: 3 × 180° = 540°
- Goldener Schnitt: φ = (1+√5)/2 ≈ 1.618
- Zentrumswinkel: 360°/5 = 72° pro Segment
- Fünfzählige Symmetrie: In der Natur weit verbreitet
Das Pentagon und der goldene Schnitt
Das regelmäßige Fünfeck ist untrennbar mit der goldenen Zahl φ verbunden:
Goldene Verhältnisse
- Diagonale : Seitenlänge = φ ≈ 1.618
- φ = (1 + √5)/2 (goldene Zahl)
- Diagonale = a · φ
- Alle Formeln enthalten √5
Pentagramm-Magie
- Fünfzackiger Stern im Pentagon
- Unendlich viele goldene Schnitte
- Selbstähnliche Strukturen
- Symbol der Perfektion
Das Fünfeck in der Natur
Die Fünfzähligkeit ist ein fundamentales Prinzip der lebendigen Natur:
Pflanzenwelt
- Fünfblättrige Blüten (Rosen, Apfel, Kirsche)
- Fünfzählige Blattstellung
- Seesterne und Seeigel
- Früchte (Apfel-Querschnitt)
Biologische Strukturen
- Menschlicher Körper (5 Finger, 5 Zehen)
- Fibonacci-Spiralen in Blumen
- Kristallstrukturen (Quasikristalle)
- Virale Kapside (Ikosaheder)
Anwendungen des regelmäßigen Fünfecks
Regelmäßige Fünfecke finden vielfältige Anwendungen:
Architektur & Politik
- Pentagon (US-Verteidigungsministerium)
- Fünfeckige Gebäude und Türme
- Historische Festungen
- Moderne Architektur-Elemente
Kunst & Design
- Pentagramm in Kunst und Religion
- Grafik-Design und Logos
- Dekorative Kunst-Objekte
- Goldener-Schnitt-Designs
Spiele & Puzzles
- Strategiespiele mit 5-eckigen Feldern
- Puzzle und Denkspiele
- Brettspielelemente
- Fünfseitige Würfel
Wissenschaft & Technik
- Quasikristalle (Nobelpreis 2011)
- Molekulare Chemie
- Optische Systeme
- Nano-Technologie
Formeln für das regelmäßige Fünfeck (Pentagon)
Flächeninhalt A
Elegante Formel mit √5 und φ
Umfang P
Einfach: 5-mal die Seitenlänge
Diagonale d
Goldener Schnitt φ = (1+√5)/2
Höhe h
Summe von Umkreis- und Innenkreisradius
Umkreisradius rₐ
Mit sin(36°) = √(10-2√5)/4
Innenkreisradius rᵢ
Apothem des Fünfecks
Seitenlänge (aus Diagonale)
Umgekehrter goldener Schnitt
Pentagramm-Beziehung
Innenstern des Pentagramms
Rechenbeispiel für ein Pentagon
Gegeben
Gesucht: Alle Eigenschaften des regelmäßigen Fünfecks
1. Grundmaße berechnen
Umfang und Flächeninhalt
2. Goldener Schnitt
Diagonale und goldene Zahl
3. Radien und Höhe
Umkreisradius, Innenkreisradius und Höhe
4. Goldene Magie
Das Pentagon offenbart die Geheimnisse der goldenen Zahl φ
Das regelmäßige Fünfeck: Goldene Geheimnisse
Das regelmäßige Fünfeck ist wohl das geheimnisvollste und faszinierendste aller Polygone. Es verbindet Mathematik, Natur, Kunst und Mystik in einzigartiger Weise und offenbart die tiefsten Geheimnisse des goldenen Schnitts. Keine andere geometrische Form zeigt so deutlich die verborgene Harmonie des Universums.
Der goldene Schnitt: φ = (1+√5)/2 ≈ 1.618
Das Pentagon ist das geometrische Zuhause der goldenen Zahl φ (Phi):
- Diagonale zu Seite: Verhältnis d:a = φ:1 (der goldene Schnitt)
- Pentagramm-Magie: Der fünfzackige Stern enthält unendlich viele goldene Schnitte
- Selbstähnlichkeit: Jedes Pentagon im Pentagramm steht im goldenen Verhältnis
- Fibonacci-Verbindung: lim(Fn+1/Fn) = φ für Fibonacci-Zahlen
- Göttliche Proportion: Die "göttliche Proportion" der Renaissance-Künstler
Das Pentagramm: Symbol der Vollkommenheit
Der fünfzackige Stern im Pentagon birgt mathematische Wunder:
Unendliche Verschachtelung
Jede Spitze des Pentagramms bildet wieder ein kleines Pentagon. Diese Struktur kann unendlich fortgesetzt werden - eine fraktale Eigenschaft.
Mystische Bedeutung
Das Pentagramm war bereits den Pythagoräern heilig. Es symbolisierte Gesundheit und wurde als Erkennungszeichen verwendet.
Goldene Kaskade
Jedes Liniensegment im Pentagramm teilt ein anderes im goldenen Schnitt. Es entstehen 4 verschiedene Längen in harmonischen Verhältnissen.
Konstruktive Eleganz
Das Pentagon kann allein mit Zirkel und Lineal konstruiert werden - eine Meisterleistung der antiken Geometrie.
Die Fünf in der Natur: Universelles Lebensprinzip
Die Fünfzähligkeit durchdringt die lebendige Natur auf allen Ebenen:
- Menschlicher Körper: 5 Sinne, 5 Finger, 5 Zehen - der Mensch als Pentagramm
- Blütenwelt: Unzählige Blüten zeigen 5-fache Symmetrie (Rosen, Apfel, Kirsche, Hibiskus)
- Meereslebewesen: Seesterne und Seeigel als lebende Pentagone
- Quasikristalle: Nobelpreis 2011 für unmögliche 5-fache Kristallsymmetrie
- Virenhüllen: Ikosaeder mit 20 dreieckigen und 12 fünfeckigen Flächen
- Botanik: Phyllotaxis - Blattstellung nach Fibonacci-Spiralen
Kulturelle und symbolische Bedeutung
Das Pentagon und Pentagramm haben tiefe kulturelle Wurzeln:
Antike und Mittelalter
Bei den Pythagoräern Symbol der Gesundheit und Perfektion. Im Mittelalter Schutz gegen böse Geister. In der Alchemie Symbol für den Äther.
Renaissance
Leonardo da Vinci und andere Künstler verwendeten den goldenen Schnitt bewusst für harmonische Proportionen in Kunst und Architektur.
Moderne Zeit
Das Pentagon als Gebäude des US-Verteidigungsministeriums. Flaggen mit Pentagrammen (USA, China, EU). Symbol für Macht und Autorität.
Wissenschaft heute
Quasikristalle, Fullerene, DNA-Struktur - das Pentagon bleibt auch in der modernen Wissenschaft zentral.
Zusammenfassung
Das regelmäßige Fünfeck ist weit mehr als nur eine geometrische Form - es ist ein Schlüssel zum Verständnis der verborgenen Harmonie des Universums. Durch seine untrennbare Verbindung zur goldenen Zahl φ offenbart es mathematische Wahrheiten, die von der Quantenphysik bis zur Kunst reichen. In der Natur allgegenwärtig, in der Kultur symbolisch aufgeladen und mathematisch von unerschöpflicher Eleganz, steht das Pentagon als lebendiger Beweis dafür, dass Schönheit und Wahrheit, Natur und Mathematik untrennbar miteinander verbunden sind. Es erinnert uns daran, dass hinter der scheinbaren Komplexität der Welt einfache, universelle Prinzipien wirken - und dass diese Prinzipien von zeitloser Schönheit sind.
|
|
|
|