Pentagramm berechnen
Rechner und Formeln für den fünfzackigen Stern des Goldenen Schnitts
Pentagramm Rechner
Das Pentagramm
Ein Pentagramm ist ein fünfzackiger Stern mit dem Goldenen Schnitt (Φ ≈ 1.618) als fundamentalem Prinzip. Symbol für Vollkommenheit.
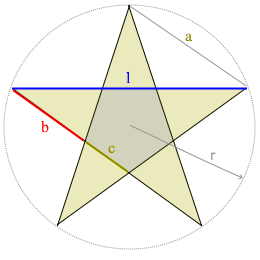
Pentagramm-Struktur
Das Pentagramm verkörpert perfekt den Goldenen Schnitt (Φ).
Vier verschiedene Längen: l, a, b, c - alle im Verhältnis Φ.
|
|
Das Pentagramm: Stern der Vollkommenheit
Das Pentagramm ist einer der faszinierendsten geometrischen Formen der Menschheit:
- Fünfzackiger Stern: Aus einem regelmäßigen Fünfeck konstruiert
- Goldener Schnitt: Φ ≈ 1.618 durchzieht alle Proportionen
- Vier Längen: l, a, b, c in perfekter harmonischer Reihe
- Universelles Symbol: In allen Kulturen als Zeichen der Vollkommenheit
- Mathematische Eleganz: Geometrie und Algebra vereint
- Spirituelle Bedeutung: Fünf Elemente, fünf Sinne, Mensch im Kosmos
Der Goldene Schnitt (Φ) im Pentagramm
Das Pentagramm ist die geometrische Verkörperung des Goldenen Schnitts:
Φ-Definition
- Göttliche Proportion
- Irrationale Zahl
- Selbstähnliche Eigenschaften
- Φ² = Φ + 1
Längenverhältnisse
- Gesamtlänge zu Pentagon-Seite
- Pentagon-Seite zu langer Sehne
- Lange Sehne zu kurzer Sehne
- Harmonische Kette von Φ-Verhältnissen
Symbolik und kulturelle Bedeutung
Das Pentagramm ist eines der mächtigsten Symbole der Menschheitsgeschichte:
Antike Traditionen
- Pythagoräer: Symbol der Vollkommenheit
- Griechen: Pentagramma, heilige Geometrie
- Römer: Venus-Stern, Liebeszeichen
- Kelten: Druiden-Stern, Naturverbindung
Universelle Bedeutungen
- Fünf Elemente: Feuer, Wasser, Erde, Luft, Äther
- Mensch: Kopf, vier Gliedmaßen im Kosmos
- Sinne: Sehen, Hören, Riechen, Schmecken, Tasten
- Vollkommenheit: Harmonie und Balance
Anwendungen des Pentagramms
Das Pentagramm findet vielfältige Anwendungen in Wissenschaft, Kunst und Kultur:
Natur & Biologie
- Blüten mit 5 Blütenblättern (Rosen, Apfelblüten)
- Seesterne und Seeigel
- Kristallstrukturen (Quasikristalle)
- Molekulare Geometrie
Kunst & Architektur
- Renaissance-Kunst (Da Vinci, Dürer)
- Kirchenarchitektur und Rosettenfenster
- Moderne Logo-Gestaltung
- Schmuck und Ornamente
Nationale Symbole
- Flaggen (USA, China, EU, viele andere)
- Militärische Abzeichen und Orden
- Staatsembleme und Wappen
- Internationale Organisationen
Moderne Technologie
- Computergrafik und 3D-Modelling
- Algorithmus-Entwicklung
- Architektur-Software (CAD)
- Künstliche Intelligenz (Musterkennung)
Formeln für das Pentagramm
Goldener Schnitt Φ
Fundamentale Konstante des Pentagramms
Seitenlänge a
Pentagon-Seitenlänge
Gesamtlänge l
Spitze zu Spitze des Sterns
Lange Sehne b
Diagonal des inneren Pentagons
Kurze Sehne c
Seite des inneren Pentagons
Umfang U
10 äußere Kanten des Sterns
Flächeninhalt A
Gesamtfläche des fünfzackigen Sterns
Umkreisradius r
Radius des umschreibenden Kreises
Rechenbeispiel für ein Pentagramm
Gegeben
Gesucht: Alle Eigenschaften des fünfzackigen Sterns
1. Φ-Berechnungen
Goldener-Schnitt-Verhältnisse
2. Weitere Längen
Kurze Sehne und Umfang
3. Φ-Verhältnisse überprüfen
Alle Verhältnisse entsprechen perfekt dem Goldenen Schnitt
4. Vollständiges Pentagramm
Das perfekte Pentagramm - Geometrie des Goldenen Schnitts
Das Pentagramm: Stern des Goldenen Schnitts
Das Pentagramm ist weit mehr als nur ein geometrisches Symbol - es ist die perfekte Verkörperung des Goldenen Schnitts und damit eine der harmonischsten Formen der Mathematik. Als fünfzackiger Stern vereint es geometrische Perfektion mit spiritueller Symbolik und zeigt, wie Mathematik und Mystik, Wissenschaft und Kunst, in einer einzigen eleganten Form zusammenfließen können.
Der Goldene Schnitt: Gottes Geometrie
Das Pentagramm ist die geometrische Manifestation des Goldenen Schnitts:
- Φ = (1+√5)/2 ≈ 1.618: Die göttliche Proportion durchzieht jede Linie
- Harmonische Kette: l:a = a:b = b:c = Φ
- Selbstähnlichkeit: Jedes kleinere Pentagon reproduziert die gleichen Verhältnisse
- Irrationale Schönheit: Φ ist irrational, doch erschafft perfekte Harmonie
- Fibonacci-Verbindung: lim(Fn+1/Fn) = Φ für Fibonacci-Zahlen
- Spiralgeometrie: Goldene Spiralen entstehen natürlich aus Pentagon-Strukturen
Von Pythagoras zu Leonardo: Eine mathematische Reise
Die Geschichte des Pentagramms ist die Geschichte der Mathematik selbst:
Antike Entdeckungen
Die Pythagoräer entdeckten das Pentagramm als Symbol der Vollkommenheit und erkannten darin den ersten Beweis für irrationale Zahlen - eine Entdeckung, die ihr Weltbild erschütterte.
Renaissance-Revolution
Leonardo da Vinci, Albrecht Dürer und andere Renaissance-Meister nutzten das Pentagramm, um die göttliche Geometrie in Kunst und Architektur zu manifestieren.
Moderne Mathematik
Heute verstehen wir das Pentagramm als Fenster zu Galois-Theorie, Gruppentheorie und komplexer Analysis - es verbindet elementare Geometrie mit höchster Mathematik.
Naturwissenschaftliche Relevanz
Von Quasikristallen bis zu Molekülstrukturen - das Pentagramm und der Goldene Schnitt strukturieren die Natur auf allen Ebenen.
Universelle Symbolik: Das Menschheitssymbol
Das Pentagramm transcendiert kulturelle Grenzen:
- Der Mensch im Kosmos: Da Vincis vitruvianischer Mensch zeigt die fünffache Symmetrie des Körpers
- Fünf Elemente: In fast allen Kulturen die Grundbausteine der Realität
- Fünf Sinne: Unsere Wahrnehmungskanäle zur Welt
- Venus-Zyklus: Die Planetenbahn der Venus zeichnet ein Pentagramm an den Himmel
- Biologische Fünfheit: Fünfblättrige Blüten, fünfstrahlige Seesterne
- Nationale Symbole: Sterne auf Flaggen repräsentieren Ideale und Werte
Moderne Anwendungen: Vom Labor zum Bildschirm
Das Pentagramm prägt unsere moderne Welt:
Wissenschaft und Technologie
Quasikristall-Forschung, Molekulardesign, Computergrafik-Algorithmen und KI-Mustererkennung nutzen pentagonale Symmetrien für bahnbrechende Innovationen.
Design und Architektur
Von Apple-Logos bis zu Pentagon-Gebäuden - das Pentagramm schafft Wiedererkennungswert und ästhetische Harmonie in modernem Design.
Therapeutische Anwendungen
Kunsttherapie, Mandala-Meditation und Architektur-Psychologie nutzen die harmonisierende Wirkung pentagonaler Formen auf die menschliche Psyche.
Kulturelle Kontinuität
Als universelles Symbol für Vollkommenheit und Harmonie verbindet das Pentagramm antike Weisheit mit modernen wissenschaftlichen Erkenntnissen.
Zusammenfassung
Das Pentagramm ist die geometrische Poesie des Universums - eine Form, in der sich die tiefsten mathematischen Wahrheiten mit der menschlichen Sehnsucht nach Harmonie und Vollkommenheit vereinen. Als lebendige Manifestation des Goldenen Schnitts verkörpert es das Paradoxon, dass irrationale Zahlen zu rationaler Schönheit führen können. Von den antiken Pythagoräern, die darin die Geheimnisse der Zahlen erkannten, bis zu modernen Wissenschaftlern, die seine Prinzipien in Quasikristallen und Algorithmen anwenden, bleibt das Pentagramm ein zeitloser Beweis dafür, dass Mathematik nicht nur Berechnung ist, sondern Sprache der Schönheit, Brücke zwischen Verstand und Gefühl, Fenster zur kosmischen Ordnung. In einer Welt voller Komplexität erinnert uns der fünfzackige Stern daran, dass wahre Eleganz in der Einfachheit liegt - und dass die schönsten Wahrheiten oft die einfachsten sind: Φ.
|
|
|
|