Pentagonal Cupola Calculator
Calculator and formulas for a pentagonal cupola (Johnson solid J5)
Pentagonal Cupola Calculator
The Pentagonal Cupola
The pentagonal cupola is a Johnson solid with a decagon base and pentagon top (J5).
Pentagonal Cupola Properties
The elegant cupola: Decagon base, pentagon top, 5 squares and 5 triangles
Cupola Structure
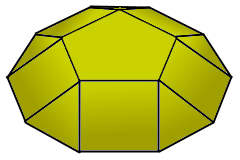
The elegant cupola structure.
Decagon base with pentagon top.
|
|
What is a Pentagonal Cupola?
A pentagonal cupola is an elegant Johnson solid:
- Definition: Johnson solid J5
- Base: Regular decagon (10 sides)
- Top: Regular pentagon (5 sides)
- Sides: 5 squares + 5 triangles
- All edges: Same length
- Shape: Truncated pyramid cupola
Geometric Properties of the Pentagonal Cupola
The pentagonal cupola shows remarkable geometric properties:
Basic Parameters
- Decagon base: Regular 10-sided polygon
- Pentagon top: Regular 5-sided polygon
- Square faces: 5 congruent squares
- Triangle faces: 5 equilateral triangles
Special Properties
- Johnson solid: One of the 92 Johnson solids
- Convex polyhedron: All faces convex
- Cupola structure: Truncated pyramid form
- Edge uniformity: All edges equal length
Mathematical Relationships
The pentagonal cupola follows elegant mathematical laws:
Volume Formula
Formula with √5 (golden ratio). Volume ≈ 2.3241 · a³.
Surface Area Formula
Advanced formula with √3 and √5. Surface ≈ 16.5798 · a².
Applications of the Pentagonal Cupola
Pentagonal cupolas find applications in various fields:
Architecture & Engineering
- Dome structures
- Cupola roofing systems
- Architectural transitions
- Decorative elements
Science & Technology
- Crystal structures
- Molecular geometry
- Materials research
- Optical components
Education & Teaching
- Geometry education
- Golden ratio studies
- 3D modeling courses
- Mathematical demonstrations
Art & Design
- Sculptural works
- Architectural art
- Decorative objects
- Geometric jewelry
Pentagonal Cupola Formulas
Volume (V)
Formula involving the golden ratio √5
Surface Area (S)
Complex formula with nested radicals
Height (h)
Height formula with golden ratio
Circumradius (r)
Circumradius with golden ratio
Pentagonal Cupola Parameters
Regular decagon
Regular pentagon
5 squares + 5 triangles
All equal length
All properties based on equal edge length a
Calculation Example for a Pentagonal Cupola
Given
Find: All properties of the pentagonal cupola
1. Volume Calculation
For a=10:
\[V = \frac{1}{6}(5 + 4\sqrt{5}) \cdot 1000\] \[V ≈ \frac{1}{6}(5 + 8.944) \cdot 1000\] \[V ≈ 2324.1\]The volume is approximately 2324.1 cubic units
2. Height Calculation
For a=10:
\[h = \sqrt{\frac{5 - \sqrt{5}}{10}} \cdot 10\] \[h ≈ \sqrt{\frac{5 - 2.236}{10}} \cdot 10\] \[h ≈ 5.257\]The height is approximately 5.257 units
3. Complete Pentagonal Cupola
The pentagonal cupola with elegant geometric proportions
The Pentagonal Cupola: Golden Ratio Elegance
The pentagonal cupola stands as one of the most elegant Johnson solids, beautifully demonstrating the mathematical harmony embedded in the golden ratio. As J5, it represents a perfect transition from a regular decagon base to a regular pentagon top, creating a structure that embodies both architectural grace and mathematical sophistication. The formulas governing this polyhedron are deeply connected to √5, the mathematical foundation of the golden ratio, making it a fascinating study in both geometry and number theory.
The Golden Ratio Connection
The pentagonal cupola showcases the beauty of golden ratio geometry:
- Pentagon connection: All pentagonal geometry involves φ (golden ratio)
- Decagon base: Natural extension of pentagonal symmetry
- Edge uniformity: All edges have identical length
- √5 formulas: Volume and surface area involve √5
- Architectural elegance: Perfect proportions for building design
- Cupola structure: Smooth transition between different polygons
- Mathematical beauty: Complex formulas with elegant results
Architectural and Mathematical Significance
Golden Ratio Mathematics
The pentagonal cupola's formulas are masterpieces of golden ratio mathematics, showing how φ appears naturally in three-dimensional geometry and creates harmonious proportions.
Architectural Applications
The cupola form has been used in architecture for millennia, providing elegant transitions between different structural elements while maintaining structural integrity.
Geometric Perfection
The smooth transition from 10-sided base to 5-sided top creates a structure that is both mathematically precise and aesthetically pleasing.
Educational Value
As a bridge between 2D polygon geometry and 3D polyhedron theory, the pentagonal cupola provides excellent educational opportunities for understanding advanced geometric concepts.
Summary
The pentagonal cupola represents the perfect fusion of mathematical elegance and practical functionality. As Johnson solid J5, it demonstrates how the golden ratio naturally emerges in three-dimensional geometry, creating structures of remarkable beauty and proportion. From its complex √5-based formulas to its practical applications in architecture and design, the pentagonal cupola continues to inspire mathematicians, architects, and artists. Its role in connecting pentagonal and decagonal geometry makes it an essential study for understanding how different polygonal forms can harmoniously combine. Whether admired for its mathematical sophistication or utilized for its architectural elegance, the pentagonal cupola stands as a testament to the enduring beauty of geometric form and the profound connections between mathematics and art.
|
|
|
|