Dreieckskuppel Rechner
Rechner und Formeln zur Dreieckskuppel (Johnson Körper J3)
Dreieckskuppel Rechner
Die Dreieckskuppel
Die Dreieckskuppel ist ein Johnson Körper (J3) mit sechseckiger Basis und dreieckiger Deckfläche.
Johnson Körper J3 Eigenschaften
Die Kuppelform: Sechseckige Basis mit dreieckiger Deckfläche
Dreieckskuppel Struktur
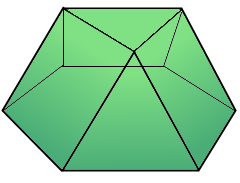
Die Dreieckskuppel mit sechseckiger Basis und dreieckiger Spitze.
Johnson Körper J3.
|
|
Was ist eine Dreieckskuppel?
Die Dreieckskuppel ist ein außergewöhnlicher Johnson Körper:
- Definition: Kuppelform mit sechseckiger Basis
- Johnson Körper: J3 in der Klassifikation
- Flächen: 1 Sechseck + 3 Quadrate + 4 Dreiecke
- Ecken: 9 Ecken insgesamt
- Kanten: 15 Kanten (alle gleich lang)
- Symmetrie: C3v-Symmetrie
Geometrische Eigenschaften der Dreieckskuppel
Die Dreieckskuppel zeigt bemerkenswerte geometrische Eigenschaften:
Grundparameter
- Flächen: 8 Flächen (1 Sechseck + 3 Quadrate + 4 Dreiecke)
- Ecken: 9 Ecken (6 am Boden, 3 in der Mitte)
- Kanten: 15 Kanten (alle gleich lang)
- Euler-Charakteristik: V - E + F = 9 - 15 + 8 = 2 ✓
Besondere Eigenschaften
- Kuppelform: Charakteristische gewölbte Struktur
- Gleichkant: Alle Kanten haben dieselbe Länge
- Regulär: Alle Dreiecke sind gleichseitig
- Konvex: Keine einspringenden Kanten oder Ecken
Mathematische Beziehungen
Die Dreieckskuppel folgt eleganten mathematischen Gesetzen:
Volumen-Formel
Kuppelvolumen mit sechseckiger Basis. Elegant mit √2 Beziehung.
Oberflächen-Formel
Kombination aus Sechseck, Quadraten und Dreiecken. Elegante √3 Beziehung.
Anwendungen der Dreieckskuppel
Dreieckskuppeln finden Anwendung in verschiedenen Bereichen:
Architektur & Bauwesen
- Kuppelkonstruktionen
- Dachaufbauten und Türme
- Gazebos und Pavillons
- Dekorative Architekturelemente
Wissenschaft & Technik
- Kristallographische Strukturen
- Molekulare Modelle
- Optische Komponenten
- Geodätische Strukturen
Bildung & Lehre
- Geometrie-Unterricht
- 3D-Geometrie-Studien
- Johnson Körper Demonstration
- Polyeder-Klassifikation
Kunst & Design
- Geometrische Skulpturen
- Moderne Kunstwerke
- Dekorative Objekte
- Schmuckdesign
Formeln zur Dreieckskuppel
Volumen (V)
Kuppelvolumen mit √2 Faktor für perfekte Proportionen
Oberfläche (S)
1 Sechseck + 3 Quadrate + 4 gleichseitige Dreiecke
Höhe (h)
Höhe mit √6 für optimale Kuppelproportionen
Johnson Körper
3. Johnson Körper in der Klassifikation
Dreieckskuppel Parameter
1⬢ + 3□ + 4△
9 Ecken
15 Kanten
C3v
Alle Eigenschaften folgen aus der Kuppelstruktur mit sechseckiger Basis
Berechnungsbeispiel für eine Dreieckskuppel
Gegeben
Gesucht: Alle Eigenschaften der Dreieckskuppel
1. Volumen-Berechnung
Für a = 10:
\[V = \frac{5\sqrt{2}}{6} \cdot 10^3\] \[V ≈ 1.1785 \cdot 1000\] \[V ≈ 1178.5\]Das Volumen beträgt etwa 1178.5 Volumeneinheiten
2. Oberflächen-Berechnung
Für a = 10:
\[S = \frac{10^2}{2}(6+5\sqrt{3})\] \[S ≈ 7.33 \cdot 100\] \[S ≈ 733\]Die Oberfläche beträgt etwa 733 Flächeneinheiten
3. Höhen-Berechnung
Für a = 10:
\[h = \frac{\sqrt{6}}{3} \cdot 10\] \[h ≈ 0.8165 \cdot 10\] \[h ≈ 8.165\]Die Höhe beträgt etwa 8.165 Längeneinheiten
4. Die perfekte Dreieckskuppel
Die Dreieckskuppel mit eleganter Kuppelform
Die Dreieckskuppel: Architektonische Eleganz in der Geometrie
Die Dreieckskuppel ist ein faszinierender Johnson Körper, der die Eleganz architektonischer Kuppelformen in der reinen Geometrie widerspiegelt. Mit ihrer sechseckigen Basis und der charakteristischen dreieckigen Deckfläche verbindet sie Stabilität mit ästhetischer Anmut. Die mathematische Schönheit liegt in den harmonischen Beziehungen mit Quadratwurzeln von 2, 3 und 6, die alle geometrischen Eigenschaften elegant miteinander verknüpfen und diese Struktur zu einem der interessantesten Beispiele für die Verbindung von Funktionalität und Form machen.
Die Geometrie der Kuppelform
Die Dreieckskuppel zeigt die Perfektion der architektonischen Geometrie:
- Kuppelstruktur: Charakteristische gewölbte Form mit stabiler Basis
- C3v-Symmetrie: Dreizählige Rotationssymmetrie mit vertikaler Spiegelebene
- Uniformität: Alle 15 Kanten haben dieselbe Länge
- Johnson Körper: J3 in der klassischen Klassifikation
- Konvexität: Alle Ecken ragen nach außen
- Stabilität: Sechseckige Basis sorgt für hohe strukturelle Integrität
- Ästhetik: Natürliche Kuppelform mit harmonischen Proportionen
Mathematische Eleganz der Kuppel
Quadratwurzel-Harmonie
Die Formeln der Dreieckskuppel zeigen elegante Beziehungen mit √2, √3 und √6, die die natürlichen Proportionen einer perfekten Kuppel beschreiben.
Architektonische Perfektion
Die Kombination von sechseckiger Basis und dreieckiger Spitze schafft eine optimale Balance zwischen Stabilität und visueller Leichtigkeit.
Strukturelle Vorteile
Die Kuppelform bietet sowohl geometrische Eleganz als auch praktische Vorteile für Bauanwendungen und Design.
Ästhetische Vollendung
Die harmonische Verbindung von Sechseck, Quadraten und Dreiecken erzeugt eine einzigartige visuelle Dynamik zwischen Ruhe und Aufwärtsstrebung.
Zusammenfassung
Die Dreieckskuppel verkörpert die perfekte Synthese zwischen architektonischer Funktionalität und mathematischer Schönheit. Ihre Struktur aus einem gleichseitigen Sechseck, drei Quadraten und vier gleichseitigen Dreiecken, beschrieben durch harmonische Quadratwurzel-Formeln, macht sie zu einem faszinierenden Studienobjekt für Architekten, Mathematiker und Designer. Als Johnson Körper J3 zeigt sie, wie geometrische Prinzipien zu praktischen und ästhetisch ansprechenden Strukturen führen können. Von der reinen Geometrie bis zur architektonischen Anwendung bleibt die Dreieckskuppel ein herausragendes Beispiel für die Kraft der geometrischen Innovation und die zeitlose Schönheit der Kuppelform.
|
|
|
|