Winkelhalbierende
Definition, Eigenschaften und Konstruktion von Winkelhalbierenden
Eine Winkelhalbierende ist eine spezielle Linie in der Geometrie, die einen Winkel in zwei gleich große Teile teilt. Sie verläuft vom Scheitelpunkt des Winkels und trennt diesen in zwei kongruente Winkel.
Winkelhalbierende sind nicht nur in der reinen Geometrie wichtig, sondern haben auch zahlreiche praktische Anwendungen in Architektur, Ingenieurwesen und Mathematik.
Grundkonzept der Winkelhalbierenden
Die Winkelhalbierende eines Winkels ist die Halbgerade, die durch den Scheitelpunkt des Winkels läuft und das Winkelfeld in zwei deckungsgleiche (kongruente) Teile teilt.
Eine Winkelhalbierende ist eine Strecke oder Gerade, die:
- Vom Scheitelpunkt des Winkels ausgeht
- Den Winkel in zwei gleich große Winkel teilt
- Mit beiden Schenkeln den gleichen Winkel bildet
- Eindeutigkeit: Zu jedem Winkel gibt es genau eine Winkelhalbierende
- Gleichheit: Die beiden entstehenden Winkel sind immer gleich groß
- Lage: Die Halbierende liegt immer im Inneren des Winkels
- Symbol: Oft mit einem Bogen markiert, der beide gleichen Winkel anzeigt
Winkelhalbierenden in Dreiecken
Im Gegensatz zu isolierten Winkeln haben Dreiecke besondere Eigenschaften bezüglich ihrer Winkelhalbierenden.
Die drei Winkelhalbierenden eines Dreiecks
Anzahl
Jedes Dreieck hat genau 3 Winkelhalbierenden
Eine für jeden Eckpunkt
Schnittpunkt
Alle 3 schneiden sich in einem Punkt: dem Inkreismittelpunkt
(Mittelpunkt des Inkreises)
Inkreis
Der Inkreis berührt alle drei Seiten des Dreiecks
Innen liegende Kreislinie
Der Punkt, in dem sich alle drei Winkelhalbierenden eines Dreiecks schneiden, wird Inkreismittelpunkt oder Incenter genannt. Dieser Punkt:
- Liegt immer im Inneren des Dreiecks
- Ist von allen drei Seiten gleich weit entfernt
- Ist der Mittelpunkt des einbeschriebenen Kreises (Inkreis)
- Hat die gleiche Entfernung zu jeder Seite (Inradius)
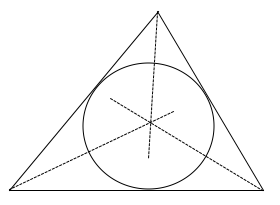
Die drei Winkelhalbierenden eines Dreiecks schneiden sich im Inkreismittelpunkt
Winkelhalbierenden vs. andere spezielle Linien
Dreiecke haben mehrere spezielle Linien. Die Winkelhalbierende unterscheidet sich von den anderen:
| Spezielle Linie | Definition | Schnittpunkt | Besonderheit |
|---|---|---|---|
| Winkelhalbierende | Halbiert den Winkel | Inkreismittelpunkt | Gleiche Entfernung zu Seiten |
| Höhe | Senkrecht zur Seite | Orthozentrum | Kann außerhalb liegen |
| Mittelsenkrechte | Rechtwinklig zur Seitenmitte | Umkreismittelpunkt | Zentrum des Umkreises |
| Seitenhalbierende (Median) | Von Ecke zur Seitenmitte | Schwerpunkt | Teilt Dreieck in gleiche Flächen |
Konstruktion einer Winkelhalbierenden
Eine Winkelhalbierende kann mit klassischen Konstruktionswerkzeugen (Lineal und Zirkel) konstruiert werden.
Konstruktionsschritte
Kreis um Scheitelpunkt
Zeichne einen Kreis um den Scheitelpunkt A des Winkels
Schnittpunkte markieren
Markiere die Schnittpunkte mit den Schenkeln als P und Q
Kreisbögen zeichnen
Zeichne Kreisbögen um P und Q mit gleichem Radius
Schnittpunkt finden
Markiere den Schnittpunkt der Kreisbögen als R
Halbierende zeichnen
Verbinde A mit R - das ist die Winkelhalbierende
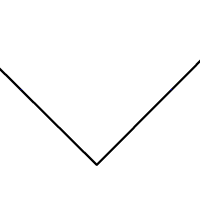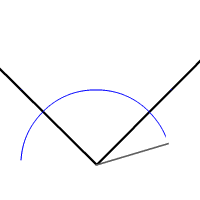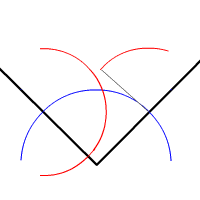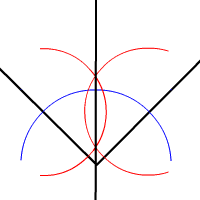
Animation der Winkelhalbierende-Konstruktion mit Zirkel und Lineal
Die Konstruktion funktioniert, weil alle Punkte auf der Windhalbierenden gleich weit entfernt von beiden Schenkeln sind. Die Punkte P und Q haben gleiche Abstände, ebenso wie die Schnittpunkte der Kreisbögen.
Praktische Beispiele
Beispiel 1: Winkelhalbierenden eines Dreiecks
Dreieck mit Winkelhalbierende
In einem Dreieck ABC mit den Winkeln:
Beispiel 2: Konstruktion einer Winkelhalbierenden
Schritt-für-Schritt Konstruktion
Gegeben: Ein Winkel von 60° mit Scheitelpunkt A
- Zeichne einen Kreis mit Mittelpunkt A
- Er schneidet die Schenkel in Punkten P und Q
- Zeichne Kreisbögen mit gleichem Radius um P und Q
- Die Bögen schneiden sich im Punkt R
- Die Linie AR ist die Winkelhalbierende
- Sie teilt den 60°-Winkel in zwei 30°-Winkel
Mathematische Eigenschaften und Sätze
Winkelhalbierende-Satz (Angle Bisector Theorem)
Wenn die Winkelhalbierende eines Winkels in einem Dreieck die gegenüberliegende Seite schneidet, dann teilt sie diese Seite im selben Verhältnis wie die anliegenden Seiten.
Wobei a und b die Teile der geteilten Seite sind, und c und d die benachbarten Seitenlängen sind.
Weitere Eigenschaften
Distanzeigenschaft
Jeder Punkt auf der Winkelhalbierenden hat den gleichen Abstand zu beiden Schenkeln des Winkels.
Inkreis-Eigenschaft
Der Inkreismittelpunkt (Schnittpunkt aller Winkelhalbierenden) ist equidistant von allen Seiten.
Spiegelsymmetrie
Die Winkelhalbierende ist die Symmetrieachse des Winkels.
Praktische Anwendungen
- Architektur: Symmetrische Anordnung von Räumen und Strukturen
- Ingenieurwesen: Konstruktion von Bauwerken mit gleichen Winkeln
- Vermessung: Genaue Winkelbestimmung im Gelände
- Computergrafik: Berechnung von Reflexionen und Lichtstrahlen
- Navigation: Bestimmung von mittleren Richtungen zwischen zwei Routen
- Optik: Berechnung von Lichtwegen und Spiegelpunkten
Tipps und häufige Fehler
- Genauigkeit: Bei der Konstruktion mit Zirkel sehr präzise arbeiten
- Gleiche Radien: Der Radius für alle Kreisbögen muss identisch sein
- Klare Markierung: Alle Schnittpunkte deutlich kennzeichnen
- Kontrolle: Die entstehenden Winkel sollten gleich groß sein (messen!)
- Inkreismittelpunkt: Immer im Inneren des Dreiecks liegen
- FALSCH: Unterschiedliche Radien für Kreisbögen verwenden | RICHTIG: Immer gleiche Radien nutzen
- FALSCH: Linie nicht durch Scheitelpunkt zeichnen | RICHTIG: Die Halbierende muss am Scheitelpunkt beginnen
- FALSCH: Mit Winkelhalbierende des Außenwinkels verwechseln | RICHTIG: Im Inneren des Winkels bleiben
- FALSCH: Ungenau mit Lineal zeichnen | RICHTIG: Mit Zirkel und Lineal präzise konstruieren
Zusammenfassung
Definition
Linie, die einen Winkel in zwei gleich große Teile teilt und vom Scheitelpunkt ausgeht
In Dreiecken
3 Winkelhalbierenden schneiden sich im Inkreismittelpunkt, der von allen Seiten gleich weit entfernt ist
Konstruktion
Mit Zirkel und Lineal durch Kreisbögen in 5 Schritten konstruierbar
|
|