Trapez
Definition, Eigenschaften und Formeln zur Berechnung von Trapezen
Ein Trapez ist ein ebenes Viereck mit zwei parallel zueinander liegenden Seiten. Die beiden parallelen Seiten werden Grundseiten oder Basen genannt. Die längere Grundseite wird oft als Basis des Trapezes bezeichnet, die beiden angrenzenden Seiten als Schenkel.
Das Trapez ist ein wichtiges geometrisches Konzept mit Anwendungen in Architektur, Ingenieurwesen und Mathematik.
Grundeigenschaften
Zwei Basen
Zwei parallele Seiten mit unterschiedlicher Länge
Schenkel
Die beiden nicht-parallelen Seiten
Höhe
Senkrechter Abstand zwischen den Basen
Mittellinie
Parallel zu Basen, Länge ist Durchschnitt der Basen
- Die an die Schenkel angrenzenden Winkel ergänzen sich zu 180°
- Jedes konvexe Trapez besitzt zwei Diagonalen, die einander im gleichen Verhältnis schneiden
- Die Mittellinie ist parallel zu den Basen und halb so lang wie deren Summe
- Ein Trapez mit gleich langen Schenkeln heißt gleichschenkliges Trapez
Formeln des Trapez
Für ein Trapez mit Basen \(a\) und \(c\) (mit \(a > c\)), Schenkeln \(b\) und \(d\), Höhe \(h\), Mittellinie \(m\) und Winkeln \(\alpha\), \(\beta\), \(\gamma\), \(\delta\):
Flächeninhalt
Mit Mittellinie:
Umfang
Mittellinie (Mittelsegment)
Mit Fläche:
Höhe
Mit Schenkeln und Winkeln:
Seitenlängen der Basen
Basis \(a\):
Basis \(c\):
Schenkellängen
Schenkel \(b\):
Schenkel \(d\):
Diagonalen
Diagonale \(e\):
Diagonale \(f\):
Innenwinkel
Praktische Beispiele
Beispiel 1: Fläche mit Basen und Höhe
Gegeben: \(a = 10\,\text{cm}\), \(c = 6\,\text{cm}\), \(h = 4\,\text{cm}\)
Beispiel 2: Mittellinie und Umfang
Gegeben: \(a = 8\,\text{cm}\), \(c = 4\,\text{cm}\), \(b = 5\,\text{cm}\), \(d = 5\,\text{cm}\)
Visualisierung
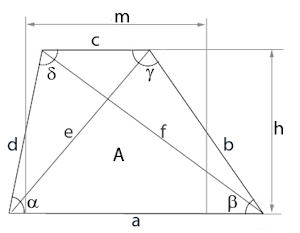
Trapez mit Basen, Schenkeln, Höhe, Diagonalen und Winkeln
Zusammenfassung
Definition
Viereck mit zwei parallelen Seiten (Basen)
Fläche
\[\displaystyle A = \frac{(a + c) \cdot h}{2}\]
Mittellinie
\[\displaystyle m = \frac{a + c}{2}\]
Umfang
\[\displaystyle U = a + b + c + d\]
|
|