Parallelogramm

Definition, Eigenschaften und Formeln zur Berechnung von Parallelogrammen

Ein Parallelogramm (auch Rhomboid genannt) ist ein konvexes ebenes Viereck, bei dem die gegenüberliegenden Seiten parallel und gleich lang sind. Das Parallelogramm ist ein Spezialfall des Trapezes und der Allgemeinfall von Rechteck und Raute.

Es ist ein fundamentales geometrisches Objekt mit zahlreichen interessanten Eigenschaften und Anwendungen.

Grundeigenschaften

Parallele Seiten

Gegenüberliegende Seiten sind parallel und gleich lang

Gleichgroße Winkel

Gegenüberliegende Winkel sind gleich groß

Supplementäre Winkel

Benachbarte Winkel ergeben zusammen 180°

Diagonalen

Diagonalen halbieren sich gegenseitig

Weitere Eigenschaften:
  • Es ist punktsymmetrisch (zweizählig drehsymmetrisch)
  • Die Diagonalen müssen nicht rechtwinklig sein
  • Das Quadrat und die Raute sind Spezialfälle des Parallelogramms
  • Das Rechteck ist ein Parallelogramm mit rechten Winkeln

Formeln des Parallelogramms

Für ein Parallelogramm mit Seitenlängen \(a\) und \(b\), Höhen \(h_a\) und \(h_b\), Winkeln \(\alpha\) und \(\beta\) sowie Diagonalen \(e\) und \(f\):

Flächeninhalt

Mit Seitenlänge und Höhe:

\[\displaystyle A = a \cdot h_a = b \cdot h_b\]

Mit Seitenlängen und Winkel:

\[\displaystyle A = a \cdot b \cdot \sin \alpha = a \cdot b \cdot \sin \beta\]

Umfang

\[\displaystyle U = 2a + 2b = 2(a + b)\]

Höhen

Höhe auf Seite \(a\):

\[\displaystyle h_a = b \cdot \sin \alpha = b \cdot \sin \beta\]
\[\displaystyle h_a = \frac{A}{a}\]

Höhe auf Seite \(b\):

\[\displaystyle h_b = a \cdot \sin \alpha = a \cdot \sin \beta\]
\[\displaystyle h_b = \frac{A}{b}\]

Diagonalen

Erste Diagonale \(e\):

\[\displaystyle e = \sqrt{a^2 + b^2 - 2ab\cos \beta}\]
\[\displaystyle e = \sqrt{a^2 + b^2 + 2ab\cos \alpha}\]

Zweite Diagonale \(f\):

\[\displaystyle f = \sqrt{a^2 + b^2 - 2ab\cos \alpha}\]
\[\displaystyle f = \sqrt{a^2 + b^2 + 2ab\cos \beta}\]

Innenwinkel

\[\displaystyle \alpha = \gamma, \quad \beta = \delta, \quad \alpha + \beta = 180°\]
\[\displaystyle \alpha = \arcsin \left(\frac{A}{ab}\right)\]

Parallelogrammgleichung

Die Summe der Quadrate der Diagonalen ist gleich der Summe der Quadrate aller Seiten:

\[\displaystyle e^2 + f^2 = 2(a^2 + b^2)\]

Praktische Beispiele

Beispiel 1: Fläche mit Seitenlängen und Winkel

Gegeben: \(a = 6\,\text{cm}\), \(b = 4\,\text{cm}\), \(\alpha = 60°\)

\[\displaystyle A = ab\sin \alpha = 6 \cdot 4 \cdot \sin(60°) = 24 \cdot 0.866 \approx 20.78\,\text{cm}^2\]

Beispiel 2: Diagonale berechnen

Gegeben: \(a = 5\,\text{cm}\), \(b = 3\,\text{cm}\), \(\alpha = 45°\)

\[\displaystyle e = \sqrt{a^2 + b^2 + 2ab\cos \alpha} = \sqrt{25 + 9 + 2(5)(3)\cos(45°)}\]
\[\displaystyle = \sqrt{34 + 30 \cdot 0.707} \approx \sqrt{55.21} \approx 7.43\,\text{cm}\]

Visualisierung

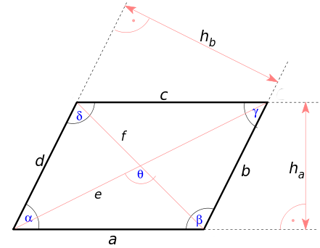
Parallelogramm Diagramm

Parallelogramm mit Seitenlängen, Höhen, Diagonalen und Winkeln

Zusammenfassung

Definition

Viereck mit parallelen und gleich langen Gegenseiten

Fläche

\[\displaystyle A = ab\sin \alpha\]

Umfang

\[\displaystyle U = 2(a + b)\]

Diagonalen

Halbieren sich gegenseitig

Parallelogramm Diagramm


Winkelhalbierende
Seitenhalbierende
Höhe eines Dreiecks
Mittelsenkrechte eines Dreiecks
Satz des Pythagoras
Pythagoreisches-Tripel (3, 4, 5)
Kreis
Quadrat
Rechteck
Raute
Parallelogramm
Trapez










Ist diese Seite hilfreich?            
Vielen Dank für Ihr Feedback!

Das tut uns leid

Wie können wir die Seite verbessern?