Quadrat
Definition, Eigenschaften und Formeln zur Berechnung von Quadraten
Ein Quadrat ist ein regelmäßiges Viereck mit vier gleich langen Seiten und vier rechten Winkeln (90°). Es ist ein Spezialfall des Rechtecks und des Rhombus und kann als das symmetrischste aller Vierecke betrachtet werden.
Das Quadrat hat zahlreiche besondere Eigenschaften und ist in Mathematik, Architektur und Anwendungen unverzichtbar.
Grundeigenschaften
Vier Seiten
Alle vier Seiten haben gleiche Länge
Vier Winkel
Alle Winkel sind 90° (rechtwinklig)
Diagonalen
Beide Diagonalen sind gleich lang und rechtwinklig
Symmetrie
4 Symmetrieachsen und Drehsymmetrie
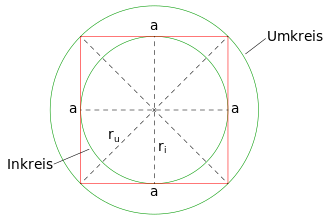
- Der Schnittpunkt der Diagonalen ist Umkreis- und Inkreismittelpunkt
- Der Flächeninhalt des Umkreises ist doppelt so groß wie der des Inkreises
- Es hat 4 Symmetrieachsen: zwei Mittelsenkrechten und zwei Diagonalen
- Es ist sowohl Sehnen- als auch Tangentenviereck
Formeln des Quadrats
Für ein Quadrat mit Seitenlänge \(a\) und Diagonale \(d\) gelten:
Flächeninhalt
Oder aus der Diagonale:
Umfang
Oder aus der Fläche:
Diagonale
Oder aus dem Umkreisradius:
Inkreisradius
Oder aus der Diagonale:
Umkreisradius
Oder aus der Diagonale:
Praktische Beispiele
Beispiel 1: Flächeninhalt und Umfang
Gegeben: Seitenlänge \(a = 5\,\text{cm}\)
Beispiel 2: Diagonale und Radien
Gegeben: Seitenlänge \(a = 4\,\text{cm}\)
Konstruktion mit gegebener Diagonale
Ein Quadrat kann mit Zirkel und Lineal konstruiert werden, wenn die Diagonale gegeben ist:
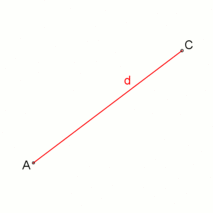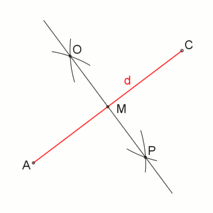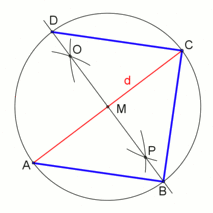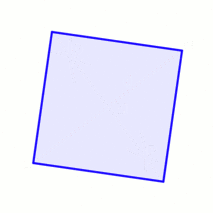
Konstruktion eines Quadrats mit gegebener Diagonale
Zusammenfassung
Definition
Regelmäßiges Viereck mit vier gleich langen Seiten und vier rechten Winkeln
Fläche
\[\displaystyle A = a^2 = \frac{d^2}{2}\]
Umfang
\[\displaystyle U = 4a\]
Diagonale
\[\displaystyle d = a\sqrt{2}\]
|
|