Rechteck
Definition, Eigenschaften und Formeln zur Berechnung von Rechtecken
Ein Rechteck ist ein Viereck, dessen Innenwinkel alle rechte Winkel (90°) sind. Es ist ein Spezialfall des Parallelogramms und damit auch des Trapezes. Ein Sonderfall des Rechtecks ist das Quadrat, bei dem alle vier Seiten gleich lang sind.
Rechtecke sind fundamental in Geometrie und Anwendungen wie Architektur, Konstruktion und Vermessung.
Grundeigenschaften
Vier Seiten
Gegenüberliegende Seiten sind gleich lang und parallel
Vier Winkel
Alle Innenwinkel sind 90° (rechtwinklig)
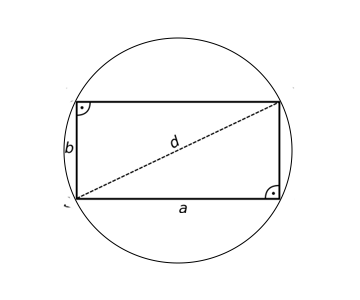
Diagonalen
Beide Diagonalen sind gleich lang
Umkreis
Es besitzt einen Umkreis (Sehnenviereck)
- Gegenüberliegende Seiten sind parallel und gleich lang
- Die Diagonalen halbieren sich gegenseitig
- Der Schnittpunkt der Diagonalen ist der Umkreismittelpunkt
- Es ist ein Spezialfall des Parallelogramms mit rechten Winkeln
Formeln des Rechtecks
Für ein Rechteck mit den Seitenlängen \(a\) und \(b\) sowie Diagonale \(d\) gelten:
Flächeninhalt
Umfang
Diagonale
Die Diagonale berechnet sich nach dem Satz des Pythagoras:
Umkreisradius
Der Umkreisradius ist die halbe Diagonale:
Praktische Beispiele
Beispiel 1: Fläche und Umfang
Gegeben: \(a = 6\,\text{cm}\), \(b = 4\,\text{cm}\)
Beispiel 2: Diagonale und Umkreisradius
Gegeben: \(a = 3\,\text{cm}\), \(b = 4\,\text{cm}\)
Goldenes Rechteck
Ein Goldenes Rechteck ist ein Rechteck mit einem speziellen Seitenverhältnis, das dem Goldenen Schnitt entspricht.
Ein Rechteck erfüllt die Bedingung des Goldenen Schnitts, wenn:
Das Seitenverhältnis ergibt sich aus dem Goldenen Schnitt:
Das Goldene Rechteck wird in Kunst, Architektur und Design geschätzt, da sein Seitenverhältnis als besonders ästhetisch empfunden wird. Dieses Verhältnis tritt auch in der Natur häufig auf.
Zusammenfassung
Definition
Viereck mit vier rechten Winkeln und gegenüberliegenden gleich langen Seiten
Fläche
\[\displaystyle A = a \cdot b\]
Umfang
\[\displaystyle U = 2(a + b)\]
Diagonale
\[\displaystyle d = \sqrt{a^2 + b^2}\]
|
|