Quadrat berechnen
Rechner und Formeln für die perfekte geometrische Form
Quadrat Rechner
Das Quadrat
Ein Quadrat ist die perfekte geometrische Form mit vier gleichen Seiten und rechten Winkeln.
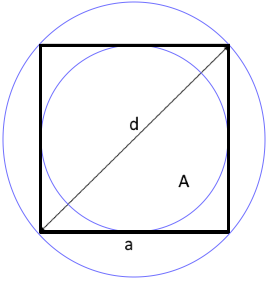
Quadrat mit Kreisen
Quadrat Eigenschaften
Perfektion: Vier gleiche Seiten, vier 90°-Winkel, √2-Diagonalen
Das Quadrat mit Innenkreis und Umkreis.
Perfekte Symmetrie in vier Achsen.
|
|
Das Quadrat: Vollendung der geometrischen Perfektion
Das Quadrat verkörpert wie keine andere Form geometrische Vollendung:
- Vier gleiche Seiten: Perfekte Gleichmäßigkeit in allen Richtungen
- Vier rechte Winkel: Jeder Winkel exakt 90°
- √2-Diagonalen: d = a × √2 ≈ 1.414 × a
- Vier Symmetrieachsen: Zwei Mittelsenkrechte + zwei Diagonalen
- Innen- und Umkreis: Umkreisfläche = 2 × Innenkreisfläche
- Maximale Effizienz: Größte Fläche bei gegebenem Umfang
Geometrische Eigenschaften des Quadrats
Die besonderen Eigenschaften des Quadrats machen es zur Grundform der Geometrie:
Symmetrie-Eigenschaften
- Vier Symmetrieachsen (Rekord unter Vierecken)
- Punktsymmetrie zum Mittelpunkt
- 90°-, 180°-, 270°-Rotationssymmetrie
- Diagonalen halbieren sich rechtwinklig
Kreis-Beziehungen
- Innenkreisradius ri = a/2
- Umkreisradius ru = d/2 = a√2/2
- Umkreisfläche = 2 × Innenkreisfläche
- Kreise berühren sich an den Seitenmitten
Die Mathematik des perfekten Quadrats
Die mathematischen Beziehungen des Quadrats sind elegant und fundamental:
√2-Verhältnisse
- Diagonale d = a × √2 ≈ 1.414 × a
- √2 ≈ 1.41421356... (irrationale Zahl)
- Umkreisradius ru = a/√2
- Fundamentale Rolle in der Zahlentheorie
Einfache Formeln
- Fläche A = a² (Quadrieren!)
- Umfang U = 4a
- Aus beliebigem Parameter alle anderen berechenbar
- Basis für Koordinatensysteme
Anwendungen des Quadrats
Quadrate sind omnipräsent in Technik, Kultur und Natur:
Architektur & Bauwesen
- Grundriss-Planung und Raumaufteilung
- Fliesen, Pflastersteine, Bodenbeläge
- Fenster, Türen und strukturelle Elemente
- Modulare Bausysteme
Digitale Welt
- Pixel in Bildschirmen und Displays
- QR-Codes und digitale Barcodes
- Game-Design (Minecraft, Tetris)
- User Interface Elemente
Kunst & Design
- Mondrian und geometrische Abstraktion
- Bauhaus-Design und Modernismus
- Logo-Design mit klaren Formen
- Grafische Raster und Layouts
Wissenschaft & Technik
- Kristallgitter und Materialwissenschaft
- Koordinatensysteme in Mathematik
- Schaltkreis-Design in Elektronik
- Bildverarbeitung und Computer Vision
Formeln für das Quadrat
Flächeninhalt A
Das klassische "Quadrieren" der Seitenlänge
Umfang U
Vier gleiche Seiten summiert
Diagonale d
Die berühmte √2-Beziehung
Seitenlänge a (Umkehrformeln)
Rückwärts-Berechnungen aus verschiedenen Parametern
Innenkreisradius ri
Hälfte der Seitenlänge
Umkreisradius ru
Hälfte der Diagonale
Innenkreisfläche Ai
Kreisfläche mit Innenkreisradius
Umkreisfläche Au
Kreisfläche mit Umkreisradius (= 2 × Ai)
Rechenbeispiel für ein Quadrat
Gegeben
Gesucht: Alle Parameter des Quadrats
1. Grundparameter
Fläche, Umfang und Diagonale
2. Kreisradien
Innen- und Umkreisradius
3. Kreisflächen
Innenkreis- und Umkreisfläche (Au = 2 × Ai)
4. Vollständiges Quadrat
Das perfekte Quadrat - geometrische Vollendung in Reinform!
Das Quadrat: Grundstein der Geometrie und Symbol der Perfektion
Das Quadrat steht seit Jahrtausenden als Symbol für Perfektion, Ordnung und mathematische Vollendung. Mit vier gleichen Seiten und rechten Winkeln verkörpert es die Essenz geometrischer Harmonie und bildet das Fundament für unzählige mathematische Konzepte - vom Pythagorischen Theorem bis zur modernen digitalen Bildverarbeitung.
Die mathematische Vollendung des Quadrats
Das Quadrat fasziniert durch seine mathematische Eleganz und Einfachheit:
- Perfekte Gleichheit: Vier identische Seiten und vier 90°-Winkel
- √2-Konstante: Diagonale = Seitenlänge × √2 (fundamentale irrationale Zahl)
- Maximale Symmetrie: Vier Symmetrieachsen - mehr als jedes andere Viereck
- Quadratische Funktion: Fläche = a² begründet den Begriff "Quadrieren"
- Kreis-Beziehungen: Umkreisfläche = 2 × Innenkreisfläche (elegante Verdopplung)
- Tesselation: Perfekte lückenlose Parkettierung der Ebene
Das Quadrat in der Kulturgeschichte
Kulturell und philosophisch hat das Quadrat eine tiefe Bedeutung erlangt:
Antike Philosophie
Platon sah im Quadrat die Verkörperung der Erde und Stabilität. Die vier Ecken repräsentierten die vier Elemente und Himmelsrichtungen.
Religiöse Symbolik
In vielen Kulturen symbolisiert das Quadrat das Materielle, Irdische - im Gegensatz zum spirituellen Kreis. Die Quadratur des Kreises wurde zum Symbol unmöglicher Vollendung.
Architekturgeschichte
Von ägyptischen Pyramiden über römische Foren bis zu modernen Stadtplänen - das Quadrat strukturiert menschliche Räume seit Jahrtausenden.
Moderne Abstraktion
Mondrians Kompositionen und Malevichs "Schwarzes Quadrat" revolutionierten die Kunst durch radikale geometrische Reduktion.
Technologische Revolution durch Quadrate
Die digitale Revolution basiert fundamental auf quadratischen Strukturen:
- Pixel-Revolution: Jeder Bildschirm besteht aus Millionen quadratischer Pixel
- QR-Codes: Quadratische Information-Encoding revolutioniert mobile Kommunikation
- Minecraft-Phänomen: Quadratische Blöcke schaffen unendliche virtuelle Welten
- Schaltkreis-Design: Integrierte Schaltungen nutzen quadratische Layouts für Effizienz
- Bildverarbeitung: Convolution-Filter arbeiten mit quadratischen Kernels
- Machine Learning: Quadratische Matrizen sind fundamental für neuronale Netze
Das Quadrat in Natur und Wissenschaft
Obwohl in der Natur seltener als Kreise und Spiralen, finden sich Quadrate in besonderen Kontexten:
Kristallographie
Viele Mineralien kristallisieren in kubischen (dreidimensional quadratischen) Systemen. Kochsalz und Pyrit zeigen quadratische Symmetrien.
Physikalische Gesetze
Das inverse Quadratgesetz (Gravitation, Elektromagnetismus) zeigt, wie fundamental quadratische Beziehungen in der Physik sind.
Biologie
Pflanzenzellen und manche Mikroorganismen zeigen quadratische Strukturen. Schachbrettblumen haben quadratische Musterungen.
Astronomie
Koordinatensysteme für Himmelskartierung nutzen quadratische Raster. CCD-Sensoren in Teleskopen haben quadratische Pixel-Arrays.
Zukunftsperspektiven der Quadrat-Geometrie
Das Quadrat bleibt auch in Zukunftstechnologien relevant:
- Quantencomputing: Qubit-Arrays in quadratischen Gittern für Quantum Error Correction
- Metamaterialien: Quadratische Unit Cells für maßgeschneiderte optische Eigenschaften
- Smart Cities: Quadratische Stadtblöcke optimieren Verkehrsfluss und Infrastruktur
- 3D-Printing: Voxel (3D-Pixel) als kubische Bausteine für komplexe Strukturen
- Blockchain: Quadratische Hash-Funktionen sichern digitale Transaktionen
- AR/VR: Quadratische Marker und Tracking-Systeme für immersive Erfahrungen
Zusammenfassung
Das Quadrat steht als zeitloses Symbol für Perfektion, Ordnung und mathematische Vollendung. Von den antiken Pyramiden über mittelalterliche Klöster bis zu modernen Bildschirmen - diese einfache Form mit vier gleichen Seiten und rechten Winkeln hat die menschliche Zivilisation geprägt. In unserer digitalen Ära gewinnt das Quadrat neue Bedeutung: Pixel strukturieren unsere visuelle Wahrnehmung, QR-Codes revolutionieren die Kommunikation, und quadratische Algorithmen treiben die künstliche Intelligenz voran. Das Quadrat erinnert uns daran, dass wahre Eleganz oft in der Einfachheit liegt - vier Linien, vier Winkel, unendliche Möglichkeiten. Es verkörpert das Streben nach Perfektion und bleibt ein fundamentaler Baustein unserer geometrischen Welt.
|
|
|
|