Addition und Subtraktion komplexer Zahlen
Grundrechenarten mit komplexen Zahlen einfach erklärt
Die Addition und Subtraktion komplexer Zahlen folgen dem gleichen Prinzip wie die Grundrechenarten mit reellen Zahlen. Dies ist das Permanenzprinzip - die Rechenregeln der reellen Zahlen bleiben auch für komplexe Zahlen gültig.
Der Schlüssel ist, dass man Real- und Imaginärteile separat behandelt, als würde man mit zwei verschiedenen Variablen rechnen.
Grundprinzip
Das Permanenzprinzip besagt, dass die Rechenregeln der reellen Zahlen auch auf komplexe Zahlen angewendet werden können.
Bei der Addition und Subtraktion komplexer Zahlen werden die Realteile und die Imaginärteile separat addiert oder subtrahiert.
Addition
(a + bi) + (c + di) = (a+c) + (b+d)i
Real- und Imaginärteile separat addieren
Subtraktion
(a + bi) - (c + di) = (a-c) + (b-d)i
Real- und Imaginärteile separat subtrahieren
Addition komplexer Zahlen
Bei der Addition werden die Realteile und die Imaginärteile jeweils zusammengefasst.
Formel für die Addition
(a + bi) + (c + di) = (a + c) + (b + d)i
Beispiel 1: Einfache Addition
Addieren Sie die komplexen Zahlen z₁ = 3 + i und z₂ = 1 - 2i
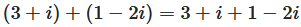
Visualisierung: (3 + i) + (1 - 2i) = 4 - i
Beispiel 2: Mit negativen Realteilen
Addieren Sie z₁ = -2 + 3i und z₂ = 1 + 2i
Beispiel 3: Mit Dezimalzahlen
Addieren Sie z₁ = 2,5 + 1,5i und z₂ = 1,5 - 0,5i
Subtraktion komplexer Zahlen
Bei der Subtraktion werden ebenfalls Real- und Imaginärteile separat subtrahiert. Wichtig ist, dass sich die Vorzeichen der zweiten Zahl umkehren!
Formel für die Subtraktion
(a + bi) - (c + di) = (a - c) + (b - d)i
Bei der Subtraktion müssen die Vorzeichen der zweiten Zahl umgekehrt werden:
(a + bi) - (c + di) = (a + bi) + (-c - di)
Beispiel 1: Einfache Subtraktion
Subtrahieren Sie z₂ = 1 - 2i von z₁ = 3 + i
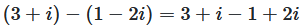
Visualisierung: (3 + i) - (1 - 2i) = 2 + 3i
Beispiel 2: Mit negativen Komponenten
Subtrahieren Sie z₂ = -1 + 2i von z₁ = 2 - 3i
Beispiel 3: Mit Dezimalzahlen
Subtrahieren Sie z₂ = 1,5 + 0,5i von z₁ = 4 + 2i
Geometrische Interpretation
Addition und Subtraktion komplexer Zahlen können auch geometrisch in der Gauß'schen Zahlenebene interpretiert werden - ähnlich wie die Vektoraddition.
Addition als Vektoraddition
Bei der Addition von z₁ + z₂ wird der Vektor von z₂ an die Spitze des Vektors von z₁ angehängt.
- Realteil des Ergebnisses = Summe der Realteile
- Imaginärteil des Ergebnisses = Summe der Imaginärteile
- Der Vektor zeigt vom Ursprung zur neuen Spitze
Subtraktion als Vektorsubtraktion
Die Subtraktion z₁ - z₂ entspricht der Differenz der Vektoren.
- Geometrisch: Vektor von z₂ zu z₁
- Realteil des Ergebnisses = Differenz der Realteile
- Imaginärteil des Ergebnisses = Differenz der Imaginärteile
Weitere Beispiele und Übersicht
| Operation | z₁ | z₂ | Realteil | Imaginärteil | Ergebnis |
|---|---|---|---|---|---|
| Addition | 2 + 3i | 1 + 2i | 2 + 1 = 3 | 3 + 2 = 5 | 3 + 5i |
| Subtraktion | 2 + 3i | 1 + 2i | 2 - 1 = 1 | 3 - 2 = 1 | 1 + i |
| Addition | 5 - 2i | -3 + 4i | 5 - 3 = 2 | -2 + 4 = 2 | 2 + 2i |
| Subtraktion | 5 - 2i | -3 + 4i | 5 - (-3) = 8 | -2 - 4 = -6 | 8 - 6i |
| Addition | -1 - i | 1 + i | -1 + 1 = 0 | -1 + 1 = 0 | 0 |
Eigenschaften von Addition und Subtraktion
Kommutativität
z₁ + z₂ = z₂ + z₁
Die Reihenfolge bei Addition ist egal
Assoziativität
(z₁ + z₂) + z₃ = z₁ + (z₂ + z₃)
Klammersetzung ist egal
Neutrales Element
z + 0 = z
Die Null (0 + 0i) ist neutral
Inverses Element
z + (-z) = 0
Jede Zahl hat ein additives Inverses
Tipps und häufige Fehler
- Schreiben Sie beide Zahlen auf: (a + bi) ± (c + di)
- Trennen Sie Real- und Imaginärteile: (a ± c) + (b ± d)i
- Beachten Sie Vorzeichen bei Subtraktion: Das Minuszeichen betrifft beide Komponenten
- Überprüfen Sie Ihr Ergebnis: Ist Real- und Imaginärteil vernünftig?
- FALSCH: (3 + 2i) - (1 + i) = 2 + 1i | RICHTIG: = 2 + i (das sind das gleiche!)
- FALSCH: Nur eine Komponente subtrahieren | RICHTIG: Beide subtrahieren
- FALSCH: (3 + 2i) - (1 + i) = (3 - 1) + (2 - 1) | RICHTIG: = (3-1) + (2-1)i = 2 + i
- FALSCH: Vorzeichenregel vergessen | RICHTIG: -(1 + i) = -1 - i
Addition und Subtraktion
Multiplizieren
Konjugieren und Dividieren
Quadratische Gleichungen
Komplexe Zahlen geometrisch darstellen
Geometrische Addition
Betrag (Absoluter Wert)
Polarform
Polarform in Normalform umrechnen
Normalform in Polarform umrechnen
Multiplikation in Polarform
|
|