Umwandlung: Normalform → Polarform
Schritt für Schritt vom kartesischen zum Polarkoordinaten-System
Die Umwandlung einer komplexen Zahl von der Normalform (z = a + bi) in die Polarform (z = r·e^(iφ)) ist ein fundamentales Konzept. Dieser Prozess erfordert die Berechnung von zwei Werten: dem Betrag r und dem Argument φ.
Schritt 1: Berechnung des Betrags
Der Betrag einer komplexen Zahl ist die Länge des Vektors vom Ursprung zum Punkt (a, b) in der Gaußschen Zahlenebene. Er wird nach dem Satz des Pythagoras berechnet.
r = |z| = √(a² + b²)
Der Betrag ist immer eine nicht-negative reelle Zahl (r ≥ 0)
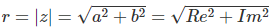
Praktisches Beispiel: z = 3 + 4i
Schritt 2: Berechnung des Arguments
Das Argument ist der Winkel φ, den der Vektor mit der positiven reellen Achse (x-Achse) einschließt. Die Berechnung hängt vom Quadranten ab, in dem die komplexe Zahl liegt.
Zwei Berechnungsmethoden
Mit Arcus Cosinus
φ = arccos(a/r)
Nutzt den Realteil und den Betrag
Mit Arcus Tangens
φ = arctan(b/a)
Nutzt das Verhältnis Imaginärteil/Realteil
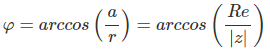
Abbildung 1: Berechnung des Arguments mit arccos
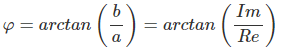
Abbildung 2: Berechnung des Arguments mit arctan
Wichtig: Quadrantenbeachten
Die arctan- und arccos-Funktionen geben nur eingeschränkte Winkelbereich zurück. Je nachdem, in welchem Quadranten die komplexe Zahl liegt, muss eine Korrektur durchgeführt werden.
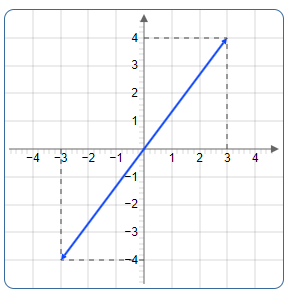
Abbildung 3: Die vier Quadranten und Beispiele
Quadrantenbeziehungen
| Quadrant | Bedingung | Winkelbereich | Korrektur |
|---|---|---|---|
| I | a > 0, b > 0 | 0° < φ < 90° | Keine Korrektur: φ = arctan(b/a) |
| II | a < 0, b > 0 | 90° < φ < 180° | φ = 180° + arctan(b/a) |
| III | a < 0, b < 0 | 180° < φ < 270° | φ = 180° + arctan(b/a) |
| IV | a > 0, b < 0 | 270° < φ < 360° | φ = 360° + arctan(b/a) |
Die arctan-Funktion gibt Werte nur zwischen -90° und 90° zurück. Um den richtigen Quadranten zu bestimmen, müssen Sie die Vorzeichen von a und b überprüfen!
Winkelformate und Bereiche
Der Winkel φ kann in verschiedenen Formaten und Bereichen angegeben werden:
0° bis 360°
Alle Winkel positiv
Standard-Bereich für Polarkoordinaten
-180° bis 180°
Negative und positive Winkel
Auch Principal Argument genannt
Radiant (Bogenmaß)
0 bis 2π oder -π bis π
Mathematischer Standard
Detaillierte Beispiele nach Quadranten
Beispiel 1: Quadrant I - z = 3 + 4i
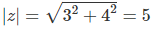
Beispiel 2: Quadrant IV - z = 3 - 4i
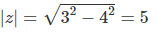
Beispiel 3: Quadrant II - z = -3 + 4i
Beispiel 4: Quadrant III - z = -3 - 4i
Übersicht aller Beispiele
| Normalform | Betrag r | Winkel φ (0-360°) | Winkel φ (-180 bis 180°) | Polarform |
|---|---|---|---|---|
| 3 + 4i | 5 | 53,13° | 53,13° | 5·e^(i·53,13°) |
| 3 - 4i | 5 | 306,87° | -53,13° | 5·e^(i·(-53,13°)) |
| -3 + 4i | 5 | 126,87° | 126,87° | 5·e^(i·126,87°) |
| -3 - 4i | 5 | 233,13° | -126,87° | 5·e^(i·(-126,87°)) |
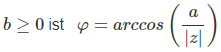
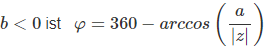
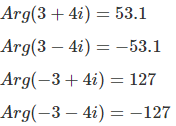
Abbildung 4: Alle vier Beispiele mit ihren Winkeln in verschiedenen Formaten
Schritt-für-Schritt Algorithmus
- Betrag berechnen: r = √(a² + b²)
- Quadrant bestimmen: Überprüfen Sie die Vorzeichen von a und b
- Vorläufigen Winkel berechnen: φ₀ = arctan(b/a)
- Winkel korrigieren: Addieren/Subtrahieren Sie 180° je nach Quadrant
- Winkelformat wählen: 0-360°, -180 bis 180°, oder Radiant
- Polarform schreiben: z = r·e^(iφ) oder z = r(cos φ + i sin φ)
Tipps und häufige Fehler
- Skizze zeichnen: Visualisieren Sie die komplexe Zahl in der Gaußschen Ebene
- Quadrant überprüfen: Das ist der häufigste Fehler!
- Konsistentes Winkelmaß: Alle Winkel in Grad ODER Radiant
- Betrag ist immer positiv: r ≥ 0 immer
- Taschenrechner konfigurieren: Auf das richtige Winkelmaß einstellen
- FALSCH: Quadrant vergessen → falscher Winkel | RICHTIG: Immer Quadrant überprüfen!
- FALSCH: arctan direkt verwenden ohne Korrektur | RICHTIG: Quadrantbeachten!
- FALSCH: Grad und Radiant vermischen | RICHTIG: Ein Format durchgehend nutzen
- FALSCH: φ = arctan(a/b) | RICHTIG: φ = arctan(b/a)
Addition und Subtraktion
Multiplizieren
Konjugieren und Dividieren
Quadratische Gleichungen
Komplexe Zahlen geometrisch darstellen
Geometrische Addition
Betrag (Absoluter Wert)
Polarform
Polarform in Normalform umrechnen
Normalform in Polarform umrechnen
Multiplikation in Polarform
|
|