Multiplikation komplexer Zahlen
Multiplikation in Normalform und Polarform
Die Multiplikation komplexer Zahlen ist komplexer als Addition und Subtraktion, folgt aber ebenfalls dem Permanenzprinzip. Wir verwenden die gleichen Rechenregeln wie bei reellen Zahlen und müssen nur beachten, dass i² = -1.
Es gibt zwei wichtige Methoden zur Multiplikation: in Normalform (a + bi) und in Polarform. Wir beginnen mit der Normalform.
Grundprinzip der Multiplikation
Die Multiplikation folgt dem Permanenzprinzip: Wir multiplizieren komplexe Zahlen wie Binome und nutzen die Tatsache, dass i² = -1.
(a + bi) · (c + di) = (ac - bd) + (ad + bc)i
Diese Formel entsteht durch Ausmultiplizieren (a + bi)(c + di) und Ersetzen von i² durch -1.
Herleitung der Formel
Multiplikation in Normalform
Beispiel 1: Einfache Multiplikation
Multiplizieren Sie die komplexen Zahlen z₁ = 3 + i und z₂ = 1 - 2i
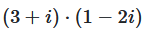
Visualisierung: Ausmultiplizieren (3 + i)(1 - 2i)
Beispiel 2: Mit negativen Komponenten
Multiplizieren Sie z₁ = 2 - 3i und z₂ = -1 + 2i
Beispiel 3: Zwei rein imaginäre Zahlen
Multiplizieren Sie z₁ = 2i und z₂ = 3i
Das Produkt zweier rein imaginärer Zahlen ist immer reell! Das liegt daran, dass (bi) · (di) = bdi² = bd(-1) = -bd.
Direkte Formel-Methode
Statt immer auszumultiplizieren, können wir auch direkt die Formel nutzen:
(a + bi) · (c + di) = (ac - bd) + (ad + bc)i
Beispiel mit direkter Formel
Multiplizieren Sie z₁ = 3 + i und z₂ = 1 - 2i mit der Formel
Weitere Beispiele und Spezialfälle
| z₁ | z₂ | z₁ · z₂ | Besonderheit |
|---|---|---|---|
| 1 + i | 1 - i | 1 - i + i - i² = 1 + 1 = 2 | Konjugierte ergeben reelle Zahl |
| 2 + 3i | 1 | 2 + 3i | Multiplikation mit 1 neutral |
| 3 + 4i | i | 3i + 4i² = 3i - 4 = -4 + 3i | Multiplikation mit i dreht um 90° |
| 1 + i | 1 + i | 1 + i + i + i² = 1 + 2i - 1 = 2i | (1+i)² = 2i |
| a + bi | a - bi | a² + b² | Produkt mit konjugierter = Betrag² |
Eigenschaften der Multiplikation
Kommutativität
z₁ · z₂ = z₂ · z₁
Die Reihenfolge ist egal
Assoziativität
(z₁ · z₂) · z₃ = z₁ · (z₂ · z₃)
Klammersetzung ist egal
Neutrales Element
z · 1 = z
Die Eins ist neutral
Inverses Element
z · (1/z) = 1 (für z ≠ 0)
Jede Zahl hat ein multiplikatives Inverses
Distributivgesetz
z₁(z₂ + z₃) = z₁z₂ + z₁z₃
Multiplizieren ist distributiv über Addition
Mit Konjugierter
z · z̄ = |z|²
Produkt = Quadrat des Betrags
Multiplikation in Polarform
Die Multiplikation ist in Polarform deutlich einfacher! Wenn eine komplexe Zahl als z = r·e^(iφ) geschrieben wird:
z₁ · z₂ = r₁ · r₂ · e^(i(φ₁ + φ₂))
In Worte: Beträge multiplizieren, Winkel addieren!
- Betrag des Produkts = Produkt der Beträge: |z₁ · z₂| = |z₁| · |z₂|
- Winkel des Produkts = Summe der Winkel: arg(z₁ · z₂) = arg(z₁) + arg(z₂)
- Geometrisch: Rotation und Skalierung kombiniert
Praktische Anwendungen
Elektrotechnik
- Impedanz: Z = R + iX (Widerstand und Reaktanz)
- Leistungsberechnung: S = V · I* (konjugiert komplexe Größen)
- Filter: Frequenzgang durch komplexe Übertragungsfunktion
Signalverarbeitung
- Fourier-Transformation: Multiplikation komplexer Exponentiellen
- Laplace-Transformation: Systemanalyse mit komplexen Funktionen
- Filter-Design: Polverlagerung durch komplexe Polynome
Quantenmechanik
- Wellenfunktionen: Ψ(x,t) = A·e^(i(kx-ωt))
- Operatoren: Multiplikation von Operatoren und Zuständen
Tipps und häufige Fehler
- Merken Sie sich i² = -1: Das ist der Schlüssel!
- Verwenden Sie die Formel oder multiplizieren Sie aus: Beide Methoden funktionieren
- Sammeln Sie Real- und Imaginärteile: Nicht durcheinander bringen
- Überprüfen Sie mit Betrag: |z₁ · z₂| = |z₁| · |z₂|
- Bei Polarform: Winkel immer addieren, nicht multiplizieren!
- FALSCH: i² = 1 | RICHTIG: i² = -1
- FALSCH: Nur die Realteile multiplizieren | RICHTIG: Alles ausmultiplizieren!
- FALSCH: (a + bi)(c + di) = ac + bdi | RICHTIG: = (ac - bd) + (ad + bc)i
- FALSCH: |z₁ · z₂| = |z₁| + |z₂| | RICHTIG: = |z₁| · |z₂|
- FALSCH: In Polarform: arg(z₁ · z₂) = arg(z₁) · arg(z₂) | RICHTIG: = arg(z₁) + arg(z₂)
Online-Tool
Teste deine Multiplikationen mit unserem interaktiven Rechner:
Addition und Subtraktion
Multiplizieren
Konjugieren und Dividieren
Quadratische Gleichungen
Komplexe Zahlen geometrisch darstellen
Geometrische Addition
Betrag (Absoluter Wert)
Polarform
Polarform in Normalform umrechnen
Normalform in Polarform umrechnen
Multiplikation in Polarform
|
|