Matrix Invertieren nach Cramer
Die Cramer-Regel und Inverse von 2×2 Matrizen
Die Inverse einer Matrix ist ein fundamentales Konzept in der linearen Algebra. Eine Matrixinverse funktioniert ähnlich wie der Kehrwert bei Zahlen: Wenn A · A⁻¹ = I (Einheitsmatrix), dann ist A⁻¹ die Inverse von A.
Die Cramer-Regel ist eine klassische Methode zur Berechnung von Matrixinversen und zur Lösung von linearen Gleichungssystemen. Sie ist jedoch nur für kleinere Matrizen praktisch, da die Rechenintensität mit der Größe schnell wächst.
Was ist eine Matrixinverse?
Eine Inverse Matrix ist einer Matrix A zugeordnet und wird mit A⁻¹ bezeichnet.
- Multiplikationseigenschaft: A · A⁻¹ = A⁻¹ · A = I
- I ist die Einheitsmatrix: Die "1" der Matrizenmultiplikation
- Nur für quadratische Matrizen: Nur Matrizen mit gleicher Zeilen- und Spaltenanzahl
- Nicht alle haben Inverse: Nur nicht-singuläre Matrizen sind invertierbar
Analoge zur Zahlenarithmetik
- Bei Zahlen: 5 · (1/5) = 1 — (1/5) ist die Inverse von 5
- Bei Matrizen: A · A⁻¹ = I — A⁻¹ ist die Inverse von A
- Spezialfall: 0 hat keine Inverse bei Zahlen
- Spezialfall: Singuläre Matrizen haben keine Inverse
Singuläre vs. Nicht-singuläre Matrizen
Nicht-singuläre Matrix
Hat eine Inverse
det(A) ≠ 0
Die Determinante ist ungleich Null
Singuläre Matrix
Hat KEINE Inverse
det(A) = 0
Die Determinante ist gleich Null
Bevor man versucht, eine Matrix zu invertieren, sollte man immer zuerst die Determinante berechnen. Ist die Determinante gleich Null, existiert keine Inverse und die Berechnung ist sinnlos.
Inverse einer 2×2 Matrix
Für 2×2 Matrizen gibt es eine einfache, geschlossene Formel, um die Inverse zu berechnen.
Die Formel
Wenn A = [a b; c d], dann ist
A⁻¹ = (1/(ad - bc)) · [d -b; -c a]
wobei ad - bc die Determinante ist.
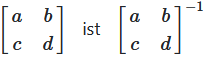
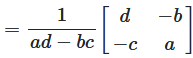
Abbildung 1: Formel für die Inverse einer 2×2 Matrix
Die drei Schritte
- Schritt 1 - Diagonale tauschen: Tausche die Diagonalelemente a und d
- Schritt 2 - Vorzeichen ändern: Ändere das Vorzeichen von b und c (nicht-diagonale Elemente)
- Schritt 3 - Durch Determinante teilen: Teile jedes Element durch (ad - bc)
Beispiel 1: Inverse einer 2×2 Matrix berechnen
Schritt-für-Schritt Berechnung
Beispiel 2: Mit Determinante ≠ 1
Matrix mit Determinante ungleich 1
Beispiel 3: Singuläre Matrix (keine Inverse)
Matrix ohne Inverse
Verifikation: A · A⁻¹ = I
Nach der Berechnung einer Inversen sollte man immer überprüfen, dass die Multiplikation wirklich die Einheitsmatrix ergibt:
Verifikation aus Beispiel 1
Cramer-Regel für größere Matrizen
Die Cramer-Regel existiert auch für 3×3, 4×4 und größere Matrizen, wird aber schnell sehr aufwändig.
- 2×2 Matrix: 1 Determinante → Sehr schnell
- 3×3 Matrix: 4 Determinanten → Machbar, aber aufwändig
- 4×4 Matrix: 5 Determinanten → Sehr zeitaufwändig
- n×n Matrix: (n+1) Determinanten → Für n > 3: Besser Andere Methoden nutzen
Alternative: Gauß-Jordan-Algorithmus
Für Matrizen größer als 2×2 (und besonders ab 3×3) ist die Gauß-Jordan-Elimination viel effizienter und praktikabler als die Cramer-Regel. Sie verwendet Zeilenoperationen, um eine Matrix systematisch in die Einheitsmatrix zu transformieren.
Zusammenfassung: Cramer-Methode für 2×2
| Schritt | Operation | Beispiel: [2 1; 5 3] |
|---|---|---|
| 1. Test | det(A) = ad - bc | 2·3 - 1·5 = 1 (≠ 0 ✓) |
| 2. Diagonale | a ↔ d tauschen | [3 1; 5 2] |
| 3. Vorzeichen | b, c negieren | [3 -1; -5 2] |
| 4. Teilen | ÷ det(A) | [3 -1; -5 2] ÷ 1 = [3 -1; -5 2] |
Tipps und häufige Fehler
- Immer Determinante testen: Berechne ad - bc zuerst! (Wenn = 0, existiert keine Inverse)
- Merksatz: "Diagonal tauschen, Nebendiagonale negieren, teilen"
- Verifikation: Immer A · A⁻¹ überprüfen, ob = I
- Brüche: Mit Brüchen arbeiten ist genauer als Dezimalzahlen
- Nur für 2×2: Für größere Matrizen andere Methoden verwenden
- FALSCH: Determinante ignorieren | RICHTIG: Immer testen, ob det ≠ 0
- FALSCH: Beide Diagonalelemente negieren | RICHTIG: Nur tauschen, nicht negieren
- FALSCH: Vergessen durch Determinante zu teilen | RICHTIG: Alle Elemente ÷ det
- FALSCH: Bei Zeilentausch rechnen | RICHTIG: Nur bei 2×2 diese Formel
Online-Rechner
Teste die Matrixinversion mit unserem interaktiven Online-Rechner:
|
|