Matrizenberechnung

Addition, Subtraktion, Multiplikation und Skalarprodukte mit Matrizen

Mit Matrizen kann genauso gerechnet werden wie mit normalen Zahlen. Es gibt allerdings spezielle Regeln, die beachtet werden müssen. Die wichtigsten Operationen sind:

  • Addition und Subtraktion
  • Multiplikation mit Skalaren (Zahlen)
  • Multiplikation von Matrizen untereinander

Um Matrizen und Skalare zu unterscheiden, werden Matrizen mit Großbuchstaben (A, B, X, Y) und Skalare mit Kleinbuchstaben (a, b, x, y) geschrieben.

Addition und Subtraktion von Matrizen

Voraussetzung: Gleiche Dimensionen

Matrizen können nur addiert oder subtrahiert werden, wenn sie die gleiche Dimension haben, d.h. die gleiche Anzahl von Zeilen und Spalten.

Addition/Subtraktion Regel:
  • Beide Matrizen müssen m × n Matrizen sein
  • Entsprechende Elemente werden addiert oder subtrahiert
  • (A + B)_ij = a_ij + b_ij
  • Das Ergebnis ist wieder eine m × n Matrix

Beispiel 1: Matrizenaddition

Addition zweier 2 × 3 Matrizen
Matrix A: [1, 2, -3] [-4, 5, 6]
Matrix B: [2, 4, 6] [3, 5, 7]
Element-weise Addition: a₁₁ + b₁₁ = 1 + 2 = 3 a₁₂ + b₁₂ = 2 + 4 = 6 a₁₃ + b₁₃ = -3 + 6 = 3 a₂₁ + b₂₁ = -4 + 3 = -1 a₂₂ + b₂₂ = 5 + 5 = 10 a₂₃ + b₂₃ = 6 + 7 = 13
Ergebnis A + B: [3, 6, 3] [-1, 10, 13]
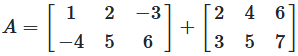
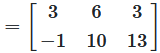
Matrizenaddition Schritt 1 Matrizenaddition Schritt 2

Abbildung 1: Visuelle Darstellung der Matrizenaddition

Beispiel 2: Matrizensubtraktion

Subtraktion zweier 2 × 3 Matrizen

Die Subtraktion funktioniert analog zur Addition: Die entsprechenden Elemente werden subtrahiert statt addiert.

Wenn A = [5, 8] und B = [2, 3], dann ist A - B = [5-2, 8-3] = [3, 5]

Weitere Informationen:

Weitere Beispiele zur Addition Weitere Beispiele zur Subtraktion

Skalarmultiplikation

Eine Matrix kann mit einem Skalar (einer gewöhnlichen Zahl) multipliziert werden. Dabei wird jedes Element der Matrix mit dieser Zahl multipliziert.

Skalarmultiplikation Regel:
  • Skalar c wird mit Matrix A multipliziert: c · A
  • Jedes Element wird mit c multipliziert: (c · A)_ij = c · a_ij
  • Das Ergebnis hat die gleiche Dimension wie A

Beispiel: Multiplikation mit Skalar 2,5

Skalarmultiplikation
Matrix A: [1, -3] [4, 7]
Skalar c = 2,5
Jedes Element mit 2,5 multiplizieren: 1 · 2,5 = 2,5 -3 · 2,5 = -7,5 4 · 2,5 = 10 7 · 2,5 = 17,5
Ergebnis 2,5 · A: [2,5, -7,5] [10, 17,5]
Skalarmultiplikation

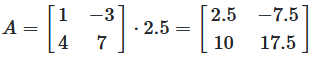
Abbildung 2: Visuelle Darstellung der Skalarmultiplikation

Eigenschaften der Skalarmultiplikation

  • Distributivität: c · (A + B) = c · A + c · B
  • Assoziativität: (c · d) · A = c · (d · A)
  • Neutrales Element: 1 · A = A
  • Nullelement: 0 · A = 0 (Nullmatrix)

Matrizenmultiplikation

Die Matrizenmultiplikation ist komplexer als Addition oder Skalarmultiplikation. Es gibt spezielle Regeln, die beachtet werden müssen.

Voraussetzung für Matrizenmultiplikation

Dimensionsregel:
  • Matrix A: m × n Dimensionen
  • Matrix B: p × q Dimensionen
  • Multiplikation möglich wenn: n = p (Spalten von A = Zeilen von B)
  • Resultat C: m × q Dimensionen
Merksatz:

(m × n) · (n × q) = (m × q)

Berechnungsmethode: Zeile-mal-Spalte

Das Element c_ij des Ergebnisses wird berechnet, indem man die i-te Zeile von A skalar mit der j-ten Spalte von B multipliziert.

Formel für Element c_ij:

c_ij = a_i1·b_1j + a_i2·b_2j + a_i3·b_3j + ... + a_in·b_nj

Die Produktsumme (Dot Product) der i-ten Zeile und j-ten Spalte

Beispiel 1: Einfache Multiplikation (2×2)

Multiplikation zweier 2 × 2 Matrizen
Matrix A (2×2): [1, 2] [3, 4]
Matrix B (2×2): [5, 6] [7, 8]
Element c₁₁ (Zeile 1 von A × Spalte 1 von B): c₁₁ = 1·5 + 2·7 = 5 + 14 = 19
Element c₁₂ (Zeile 1 von A × Spalte 2 von B): c₁₂ = 1·6 + 2·8 = 6 + 16 = 22
Element c₂₁ (Zeile 2 von A × Spalte 1 von B): c₂₁ = 3·5 + 4·7 = 15 + 28 = 43
Element c₂₂ (Zeile 2 von A × Spalte 2 von B): c₂₂ = 3·6 + 4·8 = 18 + 32 = 50
Ergebnis A × B: [19, 22] [43, 50]

Beispiel 2: Größere Matrizen (2×3) × (3×4)

Multiplikation mit unterschiedlichen Dimensionen
Matrix A (2×3): [1, 2, 3] [-1, 4, 5]
Matrix B (3×4): [2, 3, -4, 5] [-1, 0, -1, 3] [1, 2, 3, 4]
Dimensionsprüfung: A ist 2×3, B ist 3×4 → Resultat ist 2×4 ✓
Element c₁₁: 1·2 + 2·(-1) + 3·1 = 2 - 2 + 3 = 3
Element c₁₂: 1·3 + 2·0 + 3·2 = 3 + 0 + 6 = 9
Element c₁₃: 1·(-4) + 2·(-1) + 3·3 = -4 - 2 + 9 = 3
Element c₁₄: 1·5 + 2·3 + 3·4 = 5 + 6 + 12 = 23
Element c₂₁: (-1)·2 + 4·(-1) + 5·1 = -2 - 4 + 5 = -1
Element c₂₂: (-1)·3 + 4·0 + 5·2 = -3 + 0 + 10 = 7
Element c₂₃: (-1)·(-4) + 4·(-1) + 5·3 = 4 - 4 + 15 = 15
Element c₂₄: (-1)·5 + 4·3 + 5·4 = -5 + 12 + 20 = 27
Ergebnis A × B (2×4): [3, 9, 3, 23] [-1, 7, 15, 27]
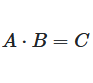
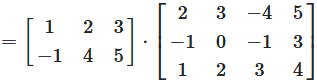
Matrizenmultiplikation Schritt 1 Matrizenmultiplikation Schritt 2 Matrizenmultiplikation Schritt 3

Abbildung 3: Visuelle Darstellung der Matrizenmultiplikation

Das Skalarprodukt (Dot Product)

Beim Berechnen eines Elements der Ergebnismatrix wird das Skalarprodukt einer Zeile und Spalte berechnet.

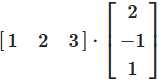
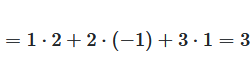
Skalarprodukt Schritt 1 Skalarprodukt Schritt 2

Abbildung 4: Berechnung des Skalarprodukts

Skalarprodukt Beispiel
Zeilenvektor: [1, 2, 3]
Spaltenvektor: [2, -1, 1]ᵀ
Skalarprodukt: 1·2 + 2·(-1) + 3·1 = 2 - 2 + 3 = 3

Eigenschaften der Matrizenmultiplikation

  • Assoziativität: (A · B) · C = A · (B · C)
  • Distributivität: A · (B + C) = A · B + A · C
  • Nicht kommutativ: A · B ≠ B · A (im allgemeinen!)
  • Identität: A · I = I · A = A (wenn I die Einheitsmatrix)
WICHTIG - Nicht kommutativ:

Die Matrizenmultiplikation ist nicht kommutativ! Das bedeutet A · B ≠ B · A. Die Reihenfolge ist entscheidend!

Weitere Informationen:

Weitere Beispiele zur Multiplikation

Zusammenfassung der Operationen

Operation Voraussetzung Methode Ergebnis
Addition Gleiche Dimension Element-weise Gleiche Dimension
Subtraktion Gleiche Dimension Element-weise Gleiche Dimension
Skalarmultiplikation Skalar und Matrix Alle Elemente × Skalar Gleiche Dimension
Matrizenmultiplikation Spalten(A) = Zeilen(B) Zeile × Spalte (Skalarprodukt) (m × n) · (n × q) = (m × q)

Tipps und häufige Fehler

Hilfreiche Tipps:
  • Dimensionen prüfen: Immer überprüfen, ob die Operationen erlaubt sind
  • Reihenfolge beachten: Bei Multiplikation ist die Reihenfolge kritisch
  • Skalarprodukt berechnen: Beim Multiplizieren einzelne Elemente sorgfältig berechnen
  • Schritt für Schritt: Große Matrizen Element für Element bearbeiten
  • Verifikation: Dimensionen des Ergebnisses überprüfen
Häufige Fehler:
  • FALSCH: Matrizen unterschiedlicher Dimension addieren | RICHTIG: Dimensionen müssen gleich sein
  • FALSCH: A · B = B · A annehmen | RICHTIG: Reihenfolge ist entscheidend!
  • FALSCH: Dimensionen nicht prüfen | RICHTIG: Vor jeder Operation überprüfen
  • FALSCH: Skalarprodukt falsch berechnen | RICHTIG: Alle Multiplikationen addieren






























Ist diese Seite hilfreich?            
Vielen Dank für Ihr Feedback!

Das tut uns leid

Wie können wir die Seite verbessern?