Zeilenoperationen in Matrizen
Elementare Zeilenoperationen und ihre Anwendungen
Elementare Zeilenoperationen sind grundlegende Transformationen, die an den Zeilen einer Matrix durchgeführt werden können. Sie sind fundamental für viele Algorithmen wie Gaußsche Elimination, Matrixinversion und die Berechnung von Determinanten.
Diese Operationen entsprechen den gleichen Transformationen, die auf Gleichungssysteme angewendet werden, um Variablen zu eliminieren und Lösungen zu finden. Die gute Nachricht: Sie ändern nicht das Wesen des zugrundeliegenden Gleichungssystems!
Die drei elementaren Zeilenoperationen
Es gibt genau drei Arten von elementaren Zeilenoperationen:
Operation 1: Zeilenaddition
Ein Vielfaches einer Zeile zu einer anderen Zeile addieren
Zeile_i → Zeile_i + k·Zeile_j
Operation 2: Skalarmultiplikation
Eine Zeile mit einem Skalar (≠ 0) multiplizieren
Zeile_i → k·Zeile_i (k ≠ 0)
Operation 3: Zeilentausch
Zwei Zeilen vertauschen
Zeile_i ↔ Zeile_j
Operation 1: Zeilenaddition (Addition eines Vielfachen)
Diese Operation addiert ein Vielfaches einer Zeile zu einer anderen Zeile.
- Operation: Zeile_i → Zeile_i + k·Zeile_j
- Bedeutung: k-mal die j-te Zeile wird zur i-ten Zeile addiert
- Alle anderen Zeilen: Bleiben unverändert
- Determinante: Ändert sich NICHT
Matrizendarstellung der Zeilenaddition
Die Operation kann durch Multiplikation mit einer modifizierten Identitätsmatrix dargestellt werden:
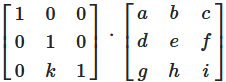
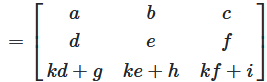
Abbildung 1: Zeilenaddition durch Matrizenmultiplikation
Praktisches Beispiel: Zeilenaddition
Anwendungen der Zeilenaddition
- Gaußsche Elimination: Eliminieren von Elementen unter der Diagonale
- LU-Zerlegung: Zerlegung in untere und obere Dreiecksmatrix
- Gleichungssysteme: Lösen von linearen Gleichungssystemen
Operation 2: Skalarmultiplikation (Zeile mit Skalar multiplizieren)
Diese Operation multipliziert eine ganze Zeile mit einem Skalar (einer Zahl), die NICHT gleich Null sein darf.
- Operation: Zeile_i → k·Zeile_i (k ≠ 0)
- Bedeutung: Jedes Element der i-ten Zeile wird mit k multipliziert
- Alle anderen Zeilen: Bleiben unverändert
- Determinante: Wird mit k multipliziert (det' = k·det)
Matrizendarstellung der Skalarmultiplikation
Diese Operation wird durch Multiplikation mit einer Diagonalmatrix dargestellt:
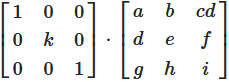
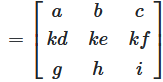
Abbildung 2: Skalarmultiplikation durch Matrizenmultiplikation
Praktisches Beispiel: Skalarmultiplikation
Anwendungen der Skalarmultiplikation
- Pivot-Normalisierung: Diagonalelemente zu 1 machen
- Normalisierung: Zeilen in spezifische Formen bringen
- Berechnung von Determinanten: Determinantenänderung tracken
Operation 3: Zeilentausch (Zwei Zeilen vertauschen)
Diese Operation vertauscht zwei ganze Zeilen miteinander.
- Operation: Zeile_i ↔ Zeile_j
- Bedeutung: Die i-te und j-te Zeile werden vertauscht
- Alle anderen Zeilen: Bleiben unverändert
- Determinante: Wechselt das Vorzeichen (det' = -det)
Matrizendarstellung des Zeilentauschs
Diese Operation wird durch Multiplikation mit einer Permutationsmatrix dargestellt:
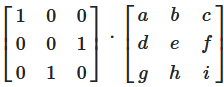
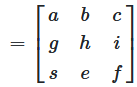
Abbildung 3: Zeilentausch durch Matrizenmultiplikation
Praktisches Beispiel: Zeilentausch
Anwendungen des Zeilentauschs
- Pivot-Auswahl: Größtes Element als Pivot auswählen
- Numerische Stabilität: Rundungsfehler minimieren
- Gaußsche Elimination: Nullen unter der Diagonale schaffen
Zusammenfassung aller Zeilenoperationen
| Operation | Notation | Determinante | Umkehrbar |
|---|---|---|---|
| Zeilenaddition | Zeile_i → Zeile_i + k·Zeile_j | det' = det | Ja (mit -k) |
| Skalarmultiplikation | Zeile_i → k·Zeile_i | det' = k·det | Ja (mit 1/k) |
| Zeilentausch | Zeile_i ↔ Zeile_j | det' = -det | Ja (repetieren) |
Auswirkungen auf Determinanten
Zeilenoperationen haben unterschiedliche Auswirkungen auf die Determinante einer Matrix:
- Zeilenaddition: det(A') = det(A) — Determinante BLEIBT gleich
- Skalarmultiplikation: det(A') = k·det(A) — Determinante wird mit k multipliziert
- Zeilentausch: det(A') = -det(A) — Determinante WECHSELT Vorzeichen
Beispiel: Auswirkung auf Determinante
Anwendungen von Zeilenoperationen
1. Gaußsche Elimination
Zeilenoperationen werden verwendet, um eine Matrix in Zeilenstufenform (Row Echelon Form) zu bringen, um lineare Gleichungssysteme zu lösen.
2. Matrixinversion
Mit Zeilenoperationen kann die inverse Matrix berechnet werden, indem die Original-Matrix durch Operationen in die Einheitsmatrix transformiert wird.
3. Determinantenberechnung
Zeilenoperationen (insbesondere Zeilenaddition) können verwendet werden, um eine Matrix in Dreiecksform zu bringen und die Determinante leicht zu berechnen.
4. Rangs-Bestimmung
Der Rang einer Matrix kann durch Reduktion zu Zeilenstufenform mit Zeilenoperationen bestimmt werden.
5. Lineare Unabhängigkeit
Zeilenoperationen helfen zu bestimmen, ob Vektoren (Zeilen) linear unabhängig sind.
Elementare Matrizen
Jede Zeilenoperation kann durch Multiplikation mit einer elementaren Matrix dargestellt werden.
Eine elementare Matrix ist eine Matrix, die entsteht, wenn man auf die Einheitsmatrix eine elementare Zeilenoperation anwendet.
Wenn E die elementare Matrix ist, dann ist das Ergebnis der Operation auf A gleich dem Produkt E·A.
- Invertierbar: Alle elementaren Matrizen sind invertierbar
- Die Umkehrung: Ist auch eine elementare Matrix (entgegengesetzte Operation)
- Verwendung: E₁ · E₂ · ... · Eₙ · A = B zeigt die Sequenz von Operationen
Tipps und beste Praktiken
- Systematisch arbeiten: Führe Operationen von oben nach unten durch
- Zeilenstufenform anstreben: Nullen unter der Diagonale schaffen
- Pivots prüfen: Wähle nicht-Null-Elemente als Pivots
- Determinante verfolgen: Notiere Auswirkungen auf die Determinante
- Rückwärts arbeiten: Bei Matrixinversion rückwärts gehen
- NICHT vergessen: Bei Skalarmultiplikation mit k, multipliziert sich det mit k
- Zeilentausch: Wechselt das Vorzeichen der Determinante
- k ≠ 0: Bei Skalarmultiplikation muss k ungleich Null sein
- Reihenfolge zählt: Die Reihenfolge der Operationen kann das Ergebnis beeinflussen
|
|