Matrix Determinante
Berechnung und Eigenschaften von Matrixdeterminanten
Die Determinante ist eine spezielle Zahl (ein Skalar), die einer quadratischen Matrix zugeordnet wird. Sie enthält wichtige Informationen über die Matrix und wird mit |A| oder det(A) notiert.
Die Determinante ist eines der wichtigsten Konzepte in der linearen Algebra. Sie wird verwendet, um zu prüfen, ob eine Matrix invertierbar ist, zur Lösung von Gleichungssystemen (Cramer-Regel) und zur Berechnung von Volumina in geometrischen Anwendungen.
Was ist eine Determinante?
Eine Determinante ist eine Funktion, die einer quadratischen Matrix A eine Zahl zuordnet.
- Nur für quadratische Matrizen: n × n Matrizen haben eine Determinante
- Skalarwert: Die Determinante ist eine einzelne Zahl
- Notation: det(A) oder |A| oder det[A]
- Berechnung: Folgt speziellen mathematischen Regeln basierend auf der Matrixgröße
Determinante erkennen: Notation
- Matrix: Eckige Klammern [ ] oder Klammern ( )
- Determinante: Vertikale Balken | | (ähnlich Betrag)
- Beispiel: A = [1 2; 3 4] vs. det(A) = |1 2; 3 4| = -2
Determinante einer 2×2 Matrix
Für 2×2 Matrizen gibt es eine einfache Formel zur Berechnung der Determinante.
Wenn A = [a b; c d], dann ist
det(A) = ad - bc
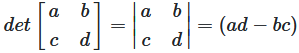
Abbildung 1: Formel für 2×2 Determinante
Praktische Beispiele
Beispiel 1: Positive Determinante
Beispiel 2: Negative Determinante
Beispiel 3: Singuläre Matrix (det = 0)
Determinante einer 3×3 Matrix
Für 3×3 Matrizen wird die Determinante durch Entwicklung nach einer Zeile oder Spalte berechnet.
Die Methode: Entwicklung nach der ersten Zeile
Man multipliziert jedes Element der ersten Zeile mit der 2×2 Unterdeterminante, die entsteht, wenn man die Zeile und Spalte dieses Elements löscht. Die Vorzeichen wechseln ab: +, -, +.
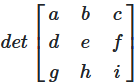
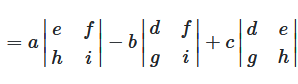
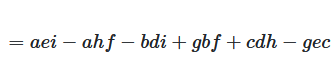
Abbildung 2: Determinante einer 3×3 Matrix durch Entwicklung
Praktisches Beispiel: 3×3 Determinante
Berechnung einer 3×3 Determinante
Determinante einer 4×4 Matrix und größer
Die gleiche Methode (Entwicklung) funktioniert auch für 4×4 Matrizen und größer, wird aber schnell sehr aufwändig.
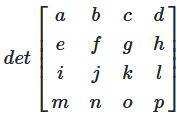
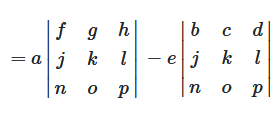
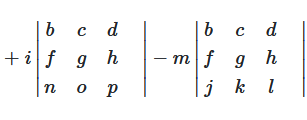
Abbildung 3: Determinante einer 4×4 Matrix durch Entwicklung
- 2×2: 1 Multiplikation
- 3×3: 3 · 2×2 Determinanten = 9 Multiplikationen
- 4×4: 4 · 3×3 Determinanten = 36 Multiplikationen
- 5×5+: Für größere Matrizen numerische Methoden bevorzugen!
Wichtige Eigenschaften von Determinanten
Determinanten haben spezielle Eigenschaften, die bei Berechnungen hilfreich sind:
Eigenschaft 1: Zeilentausch wechselt Vorzeichen
Wenn zwei Zeilen oder Spalten vertauscht werden, wechselt die Determinante das Vorzeichen.
det(A') = -det(A)
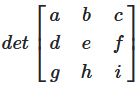
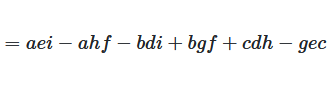
Abbildung 4: Zeilentausch wechselt das Vorzeichen
Eigenschaft 2: Skalarmultiplikation
Wenn eine Zeile oder Spalte mit einem Skalar k multipliziert wird, wird die Determinante mit k multipliziert.
det(A') = k · det(A)
Eigenschaft 3: Identische Zeilen/Spalten
Wenn zwei Zeilen oder Spalten identisch sind (oder linear abhängig), ist die Determinante Null.
det(A) = 0 wenn Zeile_i = Zeile_j
Eigenschaft 4: Zeilenaddition
Wenn man ein Vielfaches einer Zeile zu einer anderen addiert, ändert sich die Determinante NICHT.
det(A) = det(A') wenn Zeile_i → Zeile_i + k·Zeile_j
Singuläre Matrizen (det = 0)
Eine Matrix ist singulär, wenn ihre Determinante gleich Null ist. Dies hat wichtige Konsequenzen:
Nicht-singulär (det ≠ 0)
Hat eine Inverse
Matrix ist invertierbar
A⁻¹ existiert
Singulär (det = 0)
Hat KEINE Inverse
Matrix ist nicht invertierbar
A⁻¹ existiert nicht
Zeichen für singuläre Matrizen
- Null-Zeile/Spalte: Eine komplette Zeile oder Spalte ist Null
- Identische Zeilen/Spalten: Zwei Zeilen oder Spalten sind gleich
- Proportionale Zeilen/Spalten: Eine Zeile ist ein Vielfaches einer anderen
- Determinante = 0: Der direkteste Test
Determinante von Dreiecksmatrizen
Eine spezielle und wichtige Eigenschaft: Für Dreiecksmatrizen ist die Berechnung sehr einfach!
Für eine obere oder untere Dreiecksmatrix ist die Determinante das Produkt der Diagonalelemente.
det(A) = a₁₁ · a₂₂ · a₃₃ · ... · aₙₙ
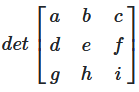
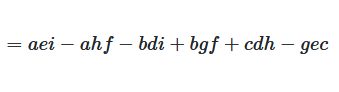
Abbildung 5: Determinante einer Dreiecksmatrix
Praktisches Beispiel
Dreiecksmatrix-Determinante
Nach Gauß-Jordan-Elimination wird eine Matrix zur Dreiecksmatrix. Mit dieser Regel kann man die Determinante sehr schnell berechnen!
Zusammenfassung: Determinanten nach Größe
| Matrixgröße | Methode | Aufwand | Beispiel |
|---|---|---|---|
| 2×2 | Formel: ad - bc | Sehr einfach ✓ | det([1 2; 3 4]) = -2 |
| 3×3 | Entwicklung nach Zeile | Machbar ✓ | Benötigt 3 · 2×2 Determinanten |
| 4×4 | Entwicklung nach Zeile | Aufwändig | Benötigt 4 · 3×3 Determinanten |
| n×n (n > 4) | Numerische Methoden oder Gaussian elimination | Siehe Achtung unten | Besser Computer verwenden |
| Dreieck | Diagonalprodukt | Sehr schnell ✓✓ | 2 · 5 · 3 = 30 |
Tipps und häufige Fehler
- 2×2 merken: Formel ad - bc ist essentiell
- Vorzeichenwechsel: Bei Zeilentausch nicht vergessen: det' = -det
- Null-Zeile/Spalte: Schneller Check: Wenn vorhanden, det = 0
- Identische Zeilen: Ebenfalls sofort det = 0
- Dreiecksform: Für große Matrizen zuerst in Dreiecksform bringen
- FALSCH: ad + bc bei 2×2 | RICHTIG: ad - bc (Minus!)
- FALSCH: Vorzeichen-Muster vergessen | RICHTIG: +, -, + bei Entwicklung
- FALSCH: Zeilentausch ignorieren | RICHTIG: det' = -det
- FALSCH: Mit großen Matrizen Entwicklung nutzen | RICHTIG: Erst Gaussian elimination
Online-Rechner
Teste die Determinantenberechnung mit unserem interaktiven Online-Rechner:
|
|