Matrizenaddition

Addieren von Matrizen mit Beispielen und Regeln

Mit Matrizen kann genauso gerechnet werden wie mit normalen Zahlen. Die Addition von Matrizen folgt dabei einfachen Regeln: Die entsprechenden Elemente werden element-weise addiert.

Um Matrizen und Skalare (normale Zahlen) zu unterscheiden, werden Matrizen mit Großbuchstaben (A, B, X, Y) und Skalare mit Kleinbuchstaben (a, b, x, y) geschrieben.

Voraussetzungen für die Addition

Nicht alle Matrizen können miteinander addiert werden. Es gibt eine grundlegende Bedingung:

Dimensionsbedingung:
  • Gleiche Zeilenanzahl: Beide Matrizen müssen die gleiche Anzahl von Zeilen haben
  • Gleiche Spaltenanzahl: Beide Matrizen müssen die gleiche Anzahl von Spalten haben
  • Notation: Wenn A eine m × n Matrix ist, muss B auch eine m × n Matrix sein
  • Ergebnis: Die Summenmatrix ist ebenfalls eine m × n Matrix

Beispiele: Welche Matrizen können addiert werden?

✓ Diese Matrizen können addiert werden:

Matrix A: 2 × 3 (2 Zeilen, 3 Spalten)

Matrix A 2×3

Matrix B: 2 × 3 (2 Zeilen, 3 Spalten)

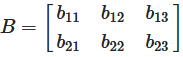
Matrix B 2×3

Grund: Beide Matrizen haben die gleichen Dimensionen (2 × 3) → Addition möglich ✓

✗ Diese Matrizen können NICHT addiert werden:

Matrix A: 2 × 3 (2 Zeilen, 3 Spalten)

Matrix A 2×3

Matrix B: 2 × 2 (2 Zeilen, 2 Spalten)

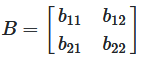
Matrix B 2×2

Grund: Die Matrizen haben unterschiedliche Dimensionen (2 × 3 vs. 2 × 2) → Addition NICHT möglich ✗

Die Additionsregel

Wenn die Dimensionen übereinstimmen, wird die Addition element-weise durchgeführt.

Additionsformel:

(A + B)_ij = a_ij + b_ij

Das Element in Zeile i und Spalte j der Summenmatrix ist die Summe der entsprechenden Elemente aus A und B.

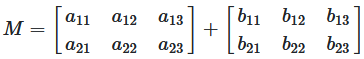
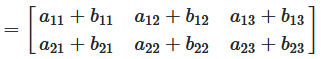
Matrizenaddition Allgemein Schritt 1 Matrizenaddition Allgemein Schritt 2

Abbildung 1: Allgemeine Formel für die Matrizenaddition

Detaillierte Beispiele

Beispiel 1: 2 × 3 Matrizen addieren

Schritt-für-Schritt Berechnung
Matrix A: [1, 2, -3] [-4, 5, 6]
Matrix B: [2, 4, 6] [3, 5, 7]
Dimensionsprüfung: A ist 2 × 3, B ist 2 × 3 → Addition möglich ✓
Element (1,1): a₁₁ + b₁₁ = 1 + 2 = 3
Element (1,2): a₁₂ + b₁₂ = 2 + 4 = 6
Element (1,3): a₁₃ + b₁₃ = -3 + 6 = 3
Element (2,1): a₂₁ + b₂₁ = -4 + 3 = -1
Element (2,2): a₂₂ + b₂₂ = 5 + 5 = 10
Element (2,3): a₂₃ + b₂₃ = 6 + 7 = 13
Resultat A + B: [3, 6, 3] [-1, 10, 13]
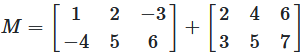
Matrizenaddition Zahlenbeispiel Schritt 1 Matrizenaddition Zahlenbeispiel Schritt 2

Abbildung 2: Konkretes Zahlenbeispiel der Matrizenaddition

Beispiel 2: 3 × 3 Matrizen addieren

Addition größerer Matrizen
Matrix A: [1, 2, 3] [4, 5, 6] [7, 8, 9]
Matrix B: [9, 8, 7] [6, 5, 4] [3, 2, 1]
Reihe 1: [1+9, 2+8, 3+7] = [10, 10, 10]
Reihe 2: [4+6, 5+5, 6+4] = [10, 10, 10]
Reihe 3: [7+3, 8+2, 9+1] = [10, 10, 10]
Resultat A + B: [10, 10, 10] [10, 10, 10] [10, 10, 10]

Eigenschaften der Matrizenaddition

Kommutativität

A + B = B + A

Die Reihenfolge ist egal

Assoziativität

(A + B) + C = A + (B + C)

Klammern können verschoben werden

Neutrales Element

A + 0 = A

Addition mit Nullmatrix ändert nichts

Inverses Element

A + (-A) = 0

Addieren mit der Negativen ergibt Nullmatrix

Die Summenmatrix

Das Resultat der Addition zweier Matrizen wird Summenmatrix genannt.

Charakteristiken der Summenmatrix:
  • Dimensionen: Hat die gleiche Anzahl von Zeilen und Spalten wie die Ausgangsmatrizen
  • Elemente: Jedes Element ist die Summe der entsprechenden Elemente
  • Notation: Wird oft mit C = A + B bezeichnet
  • Eindeutigkeit: Es gibt nur eine Summenmatrix für gegebene A und B

Zusammenfassung

Aspekt Beschreibung
Voraussetzung Beide Matrizen müssen die gleiche Dimension (m × n) haben
Methode Element-weise Addition: (A + B)_ij = a_ij + b_ij
Ergebnis Summenmatrix mit gleicher Dimension (m × n)
Kommutativität A + B = B + A ✓
Assoziativität (A + B) + C = A + (B + C) ✓

Tipps und häufige Fehler

Hilfreiche Tipps:
  • Dimensionen überprüfen: Vor der Addition immer die Dimensionen kontrollieren
  • Systematisch vorgehen: Element für Element, Zeile für Zeile bearbeiten
  • Vorzeichen beachten: Negative Zahlen korrekt addieren
  • Reihenfolge: Die Reihenfolge ist egal (kommutativ), aber systematisch arbeiten
  • Verifikation: Ergebnis überprüfen, ob alle Elemente korrekt berechnet sind
Häufige Fehler:
  • FALSCH: Matrizen unterschiedlicher Dimension addieren | RICHTIG: Dimensionen müssen gleich sein!
  • FALSCH: Elemente aus verschiedenen Positionen addieren | RICHTIG: Nur entsprechende Elemente addieren
  • FALSCH: Alle Elemente als Ganzes addieren | RICHTIG: Element-weise Addition
  • FALSCH: Vorzeichen verwechseln | RICHTIG: Vorzeichen sorgfältig beachten

Online-Rechner

Teste deine Matrizenaddition mit unserem interaktiven Online-Rechner:





















Ist diese Seite hilfreich?            
Vielen Dank für Ihr Feedback!

Das tut uns leid

Wie können wir die Seite verbessern?