Snub Cube Calculator

Online calculator and formulas for calculating a snub cube

Snub Cube Calculator

The Snub Cube

A Snub Cube is a unique Archimedean solid with chiral symmetry and 38 faces.

Enter Known Parameter
Which parameter is known?
Value of the selected parameter
Snub Cube Properties

Chiral Archimedean Solid: Exists in left-handed and right-handed forms

38 Faces 60 Edges 24 Vertices 32 Triangles + 6 Squares
Snub Cube Calculation Results
Edge length a:
Volume V:
Surface S:
Outer radius rc:
Midsphere radius rm:

Snub Cube Structure

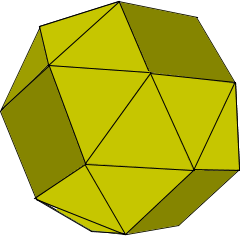
Snub Cube

A Snub Cube is the only chiral Archimedean solid.
It has 32 equilateral triangles and 6 squares.

What is a Snub Cube?

A Snub Cube is the most unique Archimedean solid:

  • Definition: The only chiral Archimedean solid
  • Faces: 32 equilateral triangles + 6 squares (38 total)
  • Chirality: Exists in left-handed and right-handed forms
  • Vertices: 24 identical vertices
  • Edges: 60 identical edges
  • Symmetry: Octahedral symmetry without reflection

Geometric Properties of the Snub Cube

The Snub Cube possesses unique geometric properties:

Basic Parameters
  • Edge length (a): Length of all 60 edges
  • Faces: 38 regular polygons (32 triangles + 6 squares)
  • Euler characteristic: V - E + F = 24 - 60 + 38 = 2
  • Dual form: Pentagonal icositetrahedron
Special Properties
  • Chirality: No reflection symmetry - exists in mirror forms
  • Vertex figure: (3.3.3.3.4) - Four triangles and one square
  • Octahedral symmetry: 24 rotational symmetry operations
  • Snub operation: Result of "snubbing" a cube

Mathematical Relationships

The Snub Cube involves the most complex mathematical relationships:

Tribonacci Constant
t ≈ 1.8393

The snub cube involves the tribonacci constant, a unique algebraic number defined by complex cubic roots.

Complex Formulas
S = 2a²(3+4√3)

Despite complex volume formulas, the surface area has a relatively simple expression with √3.

Applications of the Snub Cube

Snub Cubes find applications in specialized fields due to their chirality:

Chirality & Chemistry
  • Chiral molecular structures and enantiomers
  • Asymmetric catalysis and stereoselective synthesis
  • Pharmaceutical research and drug design
  • Chiral crystal structures and polymorphs
Advanced Materials
  • Chiral metamaterials with unique optical properties
  • Twisted nematic liquid crystals
  • Helical nanostructures and carbon nanotubes
  • Chiral photonic crystals
Optics & Physics
  • Circular dichroism and optical rotation
  • Chiral plasmonics and optical activity
  • Polarization control in photonics
  • Asymmetric scattering phenomena
Art & Design
  • Sculptural works exploring handedness
  • Architectural elements with chiral symmetry
  • Mathematical art and geometric installations
  • Puzzle design and recreational mathematics

Formulas for the Snub Cube

Tribonacci Constant t
\[t = \frac{1+\sqrt[3]{19+3\sqrt{33}} +\sqrt[3]{19-3\sqrt{33}}}{3} \approx 1.8393\]

The fundamental constant for snub cube calculations

Volume V
\[V = \frac{a^3(3\sqrt{t-1} +4\sqrt{t+1})}{3\sqrt{2-t}}\]

Complex volume formula involving the tribonacci constant

Surface S
\[S = 2a^2(3+4\sqrt{3})\]

Relatively simple surface area formula

Outer radius rc
\[r_c = a\sqrt{\frac{3-t}{4(2-t)}}\]

Circumradius involving tribonacci constant

Midsphere radius rm
\[r_m = a\sqrt{\frac{1}{4(2-t)}}\]

Midsphere radius with tribonacci constant

Edge length a (Inverse formulas)
\[a = \sqrt[3]{\frac{2V\sqrt{2-t}}{3\sqrt{t-1}+4\sqrt{t+1}}}\]

from volume

\[a = \sqrt{\frac{S}{2(3+4\sqrt{3})}}\]

from surface

\[a = \frac{r_c}{\sqrt{\frac{3-t}{4(2-t)}}}\]

from outer radius

\[a = \frac{r_m}{\sqrt{\frac{1}{4(2-t)}}}\]

from midsphere radius

Calculate edge length from other parameters

Calculation Example for a Snub Cube

Given
Edge length a = 2

Find: All properties of the Snub Cube

1. Tribonacci Constant
\[t = \frac{1+\sqrt[3]{19+3\sqrt{33}} +\sqrt[3]{19-3\sqrt{33}}}{3}\] \[t \approx 1.8393\]

The fundamental constant for all calculations

2. Surface Calculation
\[S = 2 \times 2^2 \times (3+4\sqrt{3})\] \[S = 8 \times (3+6.928)\] \[S = 8 \times 9.928\] \[S = 79.4\]

The surface area is approximately 79.4 square units

3. Volume Calculation
\[V = \frac{2^3(3\sqrt{0.839} +4\sqrt{2.839})}{3\sqrt{0.161}}\] \[V = \frac{8(2.749 + 6.747)}{1.206}\] \[V = \frac{8 \times 9.496}{1.206}\] \[V = 63.1\]

The volume is approximately 63.1 cubic units

4. Radii Calculations
\[r_c = 2\sqrt{\frac{1.161}{0.644}} = 2.67\] \[r_m = 2\sqrt{\frac{1}{0.644}} = 2.49\]

Outer radius ≈ 2.67, Midsphere radius ≈ 2.49

5. Complete Snub Cube
Edge length a = 2.00 Volume V = 63.1
Surface S = 79.4 Outer radius rc = 2.67
Midsphere radius rm = 2.49 Chiral polyhedron

The unique chiral Archimedean solid with all calculated properties

The Snub Cube: Chirality and Mathematical Complexity

The Snub Cube stands as the most mathematically complex and geometrically unique among all Archimedean solids. As the only chiral member of this distinguished family, it introduces the concept of handedness to three-dimensional geometry, while simultaneously challenging our understanding with formulas involving the mysterious tribonacci constant.

Chirality and geometric uniqueness

The Snub Cube's most remarkable property is its chirality:

  • Chiral symmetry: Exists in two non-superimposable mirror forms (left-handed and right-handed)
  • No reflection symmetry: Unlike all other Archimedean solids, it has no mirror planes
  • Face composition: 38 faces consisting of 32 equilateral triangles and 6 squares
  • Vertex configuration: Each vertex connects four triangles and one square (3.3.3.3.4)
  • Octahedral rotation group: 24 rotational symmetries without any reflections
  • Snub operation: Created by "snubbing" a cube - twisting while truncating

The tribonacci constant and mathematical complexity

Algebraic number theory

The tribonacci constant t ≈ 1.8393 is the real root of t³ - t² - t - 1 = 0, making it fundamentally different from the golden ratio. This cubic equation connects the snub cube to advanced number theory.

Complex radical expressions

The exact expression involves nested cube roots of expressions containing √33, making it one of the most complex constants in elementary geometry.

Computational challenges

The formulas require high-precision arithmetic due to the complex radical expressions. This makes the snub cube a benchmark for symbolic computation systems.

Mathematical uniqueness

Among all regular and semi-regular polyhedra, only the snub cube and snub dodecahedron require such complex algebraic constants, setting them apart from their classical cousins.

Construction and snub operation

Understanding the snub cube requires grasping the "snub" operation:

Snubbing process

Starting with a cube, the snub operation involves simultaneously truncating vertices and twisting the resulting structure. This creates the characteristic triangular faces while preserving some square faces.

Chiral generation

The twisting motion can occur in two directions (clockwise or counterclockwise), generating the two chiral forms. This inherent handedness cannot be eliminated by any rotation or reflection.

Dual relationship

Its dual, the pentagonal icositetrahedron, has 24 irregular pentagonal faces. This dual is also chiral, maintaining the handedness relationship.

Vertex regularity

Despite the complex construction, all 24 vertices remain identical, satisfying the fundamental requirement for Archimedean solids.

Applications in science and technology

The snub cube's chirality makes it valuable in specialized applications:

  • Stereochemistry: Models for understanding chiral molecules and enantiomeric relationships
  • Optical physics: Templates for chiral metamaterials with unique optical properties
  • Crystallography: Understanding chiral crystal structures and space groups
  • Materials science: Design of chiral nanomaterials and twisted structures
  • Pharmaceutical research: Drug design considering enantiomeric selectivity
  • Photonics: Chiral photonic crystals and circular dichroism devices
  • Theoretical physics: Models for parity violation and weak nuclear interactions

Mathematical formulas and computational aspects

Tribonacci relationships

All geometric properties depend on the tribonacci constant through complex radical expressions. The volume formula alone involves multiple nested square roots of expressions containing t.

Surface area simplification

Remarkably, despite the complex volume formula, the surface area S = 2a²(3+4√3) has a relatively simple form involving only √3, similar to other polyhedra with triangular faces.

Numerical precision

The nested radical expressions require careful numerical analysis to avoid precision loss. The tribonacci constant must be computed to high accuracy for reliable results.

Symbolic computation

Computer algebra systems must handle the complex radical expressions symbolically to maintain exact relationships and avoid cumulative numerical errors.

Philosophical and aesthetic significance

Handedness in nature

The snub cube embodies the concept of chirality that pervades nature, from DNA helices to spiral galaxies. It represents the mathematical foundation of handedness in three-dimensional space.

Asymmetric beauty

Its aesthetic appeal lies not in perfect symmetry but in controlled asymmetry. The snub cube demonstrates that beauty can emerge from breaking symmetry in precise, mathematical ways.

Mathematical frontier

It represents the boundary between elementary and advanced mathematics, requiring tools from algebraic number theory while remaining geometrically intuitive.

Completeness principle

The existence of chiral Archimedean solids demonstrates the completeness of the classification, showing that all possible vertex-regular forms have been discovered and categorized.

Summary

The Snub Cube stands as a monument to the richness and complexity possible within geometric mathematics. As the sole chiral Archimedean solid, it introduces the profound concept of handedness to polyhedral geometry while challenging our computational abilities with its tribonacci constant formulas. From its role in understanding molecular chirality to its applications in advanced materials science, the snub cube bridges pure mathematics and practical applications in ways that continue to inspire researchers across disciplines. Its 38 faces create not just geometric beauty but a gateway to understanding asymmetry, complexity, and the subtle mathematical structures that govern our three-dimensional world. As we advance into an era of chiral materials and asymmetric technologies, the snub cube remains our fundamental guide to understanding how mathematical sophistication and natural elegance can be perfectly unified in a single, remarkable form.

Cuboctahedron • Icosidodecahedron • Rhombicosidodecahedron • Rhombicuboctahedron • Snub cube • Truncated cube • Snub dodecahedron • Truncated cuboctahedron • Truncated dodecahedron • Truncated icosahedron • Truncated icosidodecahedron • Truncated octahedron • Truncated tetrahedron