Truncated Cuboctahedron Calculator
Calculator and formulas for calculating a truncated cuboctahedron
Truncated Cuboctahedron Calculator
The Truncated Cuboctahedron
A Truncated Cuboctahedron is a complex Archimedean solid with 26 faces: 12 squares, 8 hexagons, and 6 octagons.
Truncated Cuboctahedron Structure
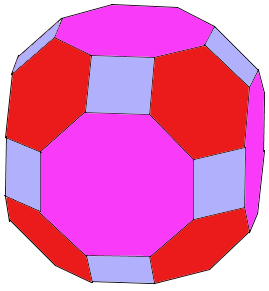
The most complex Archimedean solid with three types of faces.
It has 12 squares, 8 hexagons, and 6 octagons.
|
|
What is a Truncated Cuboctahedron?
A Truncated Cuboctahedron is the most complex Archimedean solid:
- Definition: A cuboctahedron with all vertices truncated
- Faces: 12 squares + 8 hexagons + 6 octagons (26 total)
- Construction: Created by cutting all vertices of a cuboctahedron
- Vertices: 48 identical vertices
- Edges: 72 identical edges
- Symmetry: Octahedral symmetry group
Geometric Properties of the Truncated Cuboctahedron
The Truncated Cuboctahedron exhibits the most complex geometry among Archimedean solids:
Basic Parameters
- Edge length (a): Length of all 72 identical edges
- Faces: Three types of regular polygons
- Euler characteristic: V - E + F = 48 - 72 + 26 = 2
- Dual form: Disdyakis dodecahedron
Special Properties
- Most complex Archimedean: Three face types
- Vertex figure: (4.6.8) - Square, hexagon, octagon
- Octahedral symmetry: 48 symmetry operations
- Cuboctahedron truncation: All vertices removed
Mathematical Relationships
The Truncated Cuboctahedron follows sophisticated mathematical laws:
Volume Formula
Complex volume with √2 coefficient. Factor (11+7√2) ≈ 20.9 represents truncation effect.
Surface Area
Combines areas of squares, hexagons, and octagons. Both √2 and √3 contribute to the complexity.
Applications of the Truncated Cuboctahedron
Truncated Cuboctahedra find specialized applications due to their complexity:
Advanced Materials
- Complex crystal lattice structures
- Multi-functional cage molecules
- Advanced coordination polymers
- Hierarchical nanomaterials
High-Tech Applications
- Complex 3D printing geometries
- Advanced computational meshes
- Sophisticated architectural elements
- Precision mechanical components
Research & Development
- Mathematical modeling studies
- Complex geometry algorithms
- Advanced simulation frameworks
- Theoretical polyhedra research
Educational Tools
- Advanced geometry demonstrations
- Complex symmetry studies
- Mathematical visualization
- 3D geometry education
Formulas for the Truncated Cuboctahedron
Volume V
Complex volume formula with √2 term
Surface S
Surface combining three polygon types
Outer radius rc
Circumradius with nested radical expression
Midsphere radius rm
Radius of sphere touching all edges
Edge length a (Inverse formulas)
from volume
from surface
from outer radius
from midsphere radius
Calculate edge length from other parameters
Calculation Example for a Truncated Cuboctahedron
Given
Find: All properties of the Truncated Cuboctahedron
1. Volume Calculation
The volume is approximately 2675 cubic units
2. Surface Calculation
The surface area is approximately 988 square units
3. Outer Radius
The outer radius is approximately 9.27 units
4. Midsphere Radius
The midsphere radius is approximately 9.05 units
5. Complete Truncated Cuboctahedron
The most complex Archimedean solid with all calculated properties
The Truncated Cuboctahedron: Pinnacle of Archimedean Complexity
The Truncated Cuboctahedron represents the ultimate achievement in Archimedean geometry - the most complex and sophisticated of all thirteen uniform polyhedra. This remarkable solid exemplifies how systematic mathematical operations can transform relatively simple forms into structures of breathtaking complexity while maintaining perfect symmetry and regularity. With its 26 faces comprising three distinct polygon types, it showcases the rich mathematical beauty that emerges when truncation operations are applied to already complex polyhedra.
Construction and geometric complexity
The Truncated Cuboctahedron demonstrates the highest level of constructive sophistication:
- Dual truncation process: Created by truncating the vertices of a cuboctahedron itself
- Three face types: 12 squares, 8 hexagons, and 6 octagons in perfect harmony
- Maximum vertex uniformity: Each of the 48 vertices connects exactly one face of each type
- Edge consistency: All 72 edges have identical length despite connecting different polygon types
- Octahedral symmetry: Preserves the full 48-element symmetry group of the original cuboctahedron
- Vertex configuration (4.6.8): Unique among Archimedean solids for its three-polygon vertex arrangement
Historical significance and mathematical development
Ancient recognition
While Archimedes systematically catalogued this polyhedron over 2000 years ago, its complexity made it one of the most challenging to construct physically, requiring sophisticated understanding of three-dimensional geometry.
Renaissance fascination
During the Renaissance, mathematicians like Kepler and artists like Dürer were particularly drawn to its complexity, seeing it as a culmination of geometric sophistication and a bridge between pure mathematics and artistic beauty.
Modern applications
The advent of computer graphics and 3D modeling has revealed new applications for this complex geometry in fields ranging from molecular chemistry to architectural design and advanced materials science.
Contemporary research
Modern mathematicians continue to study this polyhedron for insights into symmetry theory, group theory, and the geometric principles underlying complex three-dimensional structures.
Mathematical sophistication and formula intricacy
The truncated cuboctahedron showcases the most sophisticated mathematical relationships:
Volume complexity
The volume formula V = 2a³(11+7√2) elegantly combines rational arithmetic with irrational coefficients. The factor (11+7√2) ≈ 20.9 represents the cumulative effect of dual truncation operations on the original volume.
Surface area intricacy
The surface area S = 12a²(2+√2+√3) is unique among Archimedean solids for incorporating both √2 and √3 simultaneously, reflecting the geometric complexity of combining squares, hexagons, and octagons.
Radius formulations
Both circumradius and midsphere radius formulas involve nested radicals with √2 terms, demonstrating the deep mathematical structure underlying the truncation geometry and the sophisticated relationships between different types of vertices and faces.
Computational challenges
The mathematical complexity makes this polyhedron particularly interesting for computational geometry, requiring sophisticated algorithms for accurate calculation and 3D rendering while maintaining numerical stability.
Advanced scientific and technological applications
The complexity of the truncated cuboctahedron makes it valuable in specialized applications:
- Advanced crystallography: Framework for complex crystal structures with multiple coordination environments
- Molecular cage design: Template for sophisticated cage molecules with multiple binding sites
- Architectural innovation: Complex building elements requiring sophisticated three-face vertex connections
- 3D printing optimization: Test case for advanced additive manufacturing of complex geometries
- Computer graphics: Benchmark geometry for testing advanced rendering algorithms and mesh generation
- Materials science: Model for hierarchical materials with multiple surface orientations
- Educational demonstration: Ultimate example of geometric complexity and mathematical beauty
Construction techniques and precision requirements
Truncation precision
Creating a perfect truncated cuboctahedron requires extraordinarily precise control over the truncation process. Each vertex of the original cuboctahedron must be removed with exact depth to ensure all resulting edges have identical length.
Manufacturing complexity
The combination of three different face types creates significant manufacturing challenges, requiring sophisticated tooling and quality control to maintain the geometric relationships between squares, hexagons, and octagons.
Dual relationships
Its dual, the disdyakis dodecahedron, has 48 scalene triangular faces corresponding to the 48 vertices. This duality reveals deep connections between complex uniform and non-uniform polyhedra.
Symmetry preservation
Despite its complexity, the truncation process perfectly preserves octahedral symmetry, demonstrating how sophisticated mathematical operations can maintain underlying structural beauty.
Aesthetic and philosophical significance
Visual complexity
The truncated cuboctahedron achieves an extraordinary balance between order and complexity, creating visual forms that are simultaneously sophisticated and harmonious, challenging viewers to comprehend its three-dimensional intricacy.
Mathematical beauty
As the most complex Archimedean solid, it represents the ultimate expression of uniform polyhedra, demonstrating how mathematical principles can create forms of breathtaking beauty through systematic application of geometric rules.
Educational inspiration
This polyhedron serves as the pinnacle of three-dimensional geometric education, challenging students to understand complex relationships between different polygon types and inspiring appreciation for mathematical sophistication.
Symbolic significance
In many contexts, the truncated cuboctahedron symbolizes the achievement of maximum complexity within ordered systems, representing the potential for sophisticated outcomes through systematic mathematical processes.
Contemporary relevance and future applications
Advanced manufacturing
Modern additive manufacturing technologies are finally making it practical to create precise truncated cuboctahedra for real-world applications, opening new possibilities in engineering and design.
Computational geometry
Its complexity makes it an excellent test case for advanced algorithms in computational geometry, mesh generation, and 3D modeling software development, pushing the boundaries of geometric computation.
Materials innovation
Research into materials with truncated cuboctahedral structures is revealing new possibilities for creating substances with unique properties derived from their complex geometric organization.
Artistic inspiration
Contemporary artists and designers continue to find inspiration in its complex beauty, creating works that explore the intersection of mathematics, geometry, and aesthetic expression.
Summary
The Truncated Cuboctahedron stands as the crowning achievement of Archimedean geometry, representing the ultimate synthesis of mathematical complexity and geometric beauty. Its 26 faces, comprising three distinct polygon types in perfect harmony, demonstrate how systematic mathematical operations can create forms of extraordinary sophistication while maintaining fundamental symmetries and relationships. From its ancient recognition by Archimedes to its modern applications in advanced materials science and computational geometry, this remarkable polyhedron continues to inspire mathematicians, engineers, artists, and scientists with its perfect balance of complexity and order. As the most complex uniform polyhedron, it serves as both a testament to the power of mathematical thinking and a reminder that even the most sophisticated structures can emerge from simple, systematic principles. In an age of increasing technological complexity, the truncated cuboctahedron remains a profound example of how mathematical beauty and practical application can unite in forms that challenge our understanding while inspiring our imagination.