Truncated Icosahedron Calculator
Calculator and formulas for calculating a truncated icosahedron
Truncated Icosahedron Calculator
The Truncated Icosahedron
A Truncated Icosahedron is the most famous Archimedean solid - the classic soccer ball pattern with 12 pentagons and 20 hexagons.
Truncated Icosahedron Structure
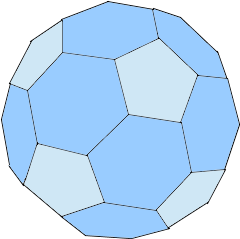
The world's most famous polyhedron - the soccer ball!
12 black pentagons and 20 white hexagons.
|
|
What is a Truncated Icosahedron?
A Truncated Icosahedron is the world's most famous polyhedron:
- Definition: An icosahedron with all 12 vertices truncated
- Faces: 12 regular pentagons + 20 regular hexagons (32 total)
- Soccer ball: The classic black and white football pattern
- Vertices: 60 identical vertices
- Edges: 90 identical edges
- Global icon: Recognized worldwide in sports
Geometric Properties of the Truncated Icosahedron
The Truncated Icosahedron combines mathematical elegance with practical perfection:
Basic Parameters
- Edge length (a): Length of all 90 identical edges
- Faces: Two types of regular polygons in perfect harmony
- Euler characteristic: V - E + F = 60 - 90 + 32 = 2
- Dual form: Pentakis dodecahedron
Special Properties
- Archimedean solid: All vertices are congruent
- Vertex figure: (5.6.6) - One pentagon and two hexagons
- Icosahedral symmetry: 120 symmetry operations
- Optimal sphericity: Excellent sphere approximation
Mathematical Relationships
The Truncated Icosahedron follows elegant mathematical laws involving the golden ratio:
Volume Formula
Volume involving √5 (golden ratio). Factor (125+43√5) ≈ 221 from icosahedral geometry.
Surface Area
Combines pentagonal and hexagonal areas. Golden ratio √5 appears in nested form.
Applications of the Truncated Icosahedron
Truncated Icosahedra are everywhere - from sports to science:
Sports & Recreation
- Classic soccer ball design (FIFA standard)
- Volleyballs and recreational balls
- Sports equipment with optimal aerodynamics
- Gaming dice and puzzle balls
Chemistry & Biology
- Fullerene C60 (Buckyballs) carbon structures
- Virus capsid architectures and proteins
- Molecular cage compounds
- Carbon nanotube caps and endohedral fullerenes
Architecture & Design
- Geodesic dome construction principles
- Spherical architectural elements
- Pavilion and exhibition structures
- Decorative panels and ceiling designs
Technology & Engineering
- Satellite design and space structures
- Radar domes and communication systems
- 3D printing and manufacturing patterns
- Computer graphics and game design
Formulas for the Truncated Icosahedron
Volume V
Volume with golden ratio √5 coefficient
Surface S
Surface combining pentagonal and hexagonal areas
Outer radius rc
Circumradius with golden ratio term
Midsphere radius rm
Radius involving golden ratio (1+√5)
Pentagon radius r5
Distance from center to pentagon face
Hexagon radius r6
Distance from center to hexagon face
Edge length a (Inverse formulas)
from volume
from surface
from outer radius
from midsphere radius
from pentagon radius
Calculate edge length from other parameters
Calculation Example for a Truncated Icosahedron
Given
Find: All properties of the famous Soccer Ball
1. Volume Calculation
The volume is approximately 55.3 cubic units
2. Surface Calculation
The surface area is approximately 72.6 square units
3. Radius Calculations
Outer radius ≈ 2.48, Midsphere radius ≈ 2.43
4. Face Radii
Pentagon radius ≈ 2.38, Hexagon radius ≈ 2.45
5. The Perfect Soccer Ball
The legendary soccer ball - perfect balance of mathematics and sports engineering
The Truncated Icosahedron: From Ancient Greece to the World Cup
The Truncated Icosahedron is undoubtedly the world's most recognizable polyhedron, transcending the boundaries between pure mathematics and popular culture. Known globally as the classic soccer ball pattern, this extraordinary Archimedean solid represents the perfect synthesis of geometric elegance, practical functionality, and universal appeal. From its ancient mathematical origins to its starring role in the world's most popular sport, it embodies how mathematical principles can achieve both aesthetic perfection and practical excellence, touching billions of lives across the globe.
The soccer ball revolution: geometry meets sport
The Truncated Icosahedron's transformation into the soccer ball represents one of the most successful applications of mathematical geometry in mass culture:
- FIFA adoption: Officially adopted for the 1970 World Cup in Mexico
- Pattern perfection: 12 black pentagons and 20 white hexagons in perfect alternation
- Optimal sphericity: Provides the best sphere approximation with flat panels
- Manufacturing advantage: Flat polygonal panels are easier to produce than curved surfaces
- Visual recognition: High contrast pattern aids in ball tracking and television visibility
- Aerodynamic efficiency: Balanced surface creates predictable flight characteristics
- Global icon: Instantly recognizable symbol of football/soccer worldwide
Mathematical elegance and golden ratio connections
Icosahedral inheritance
Born from the icosahedron, this solid inherits all the mathematical beauty of 20-faced symmetry. The truncation process transforms triangular faces into hexagons while creating pentagonal faces at the vertex positions.
Golden ratio omnipresence
The golden ratio φ = (1+√5)/2 ≈ 1.618 appears throughout the geometry, in the relationships between edge lengths, face areas, and angular measurements, connecting this practical object to the deepest mathematical constants.
Pentagon-hexagon harmony
The perfect arrangement of pentagons and hexagons follows strict mathematical rules. Each pentagon is surrounded by 5 hexagons, and each hexagon touches 3 pentagons and 3 hexagons, creating perfect vertex uniformity.
Euler's formula validation
With V=60, E=90, F=32, it perfectly satisfies Euler's polyhedron formula: V - E + F = 2, demonstrating the fundamental topological principles governing three-dimensional closed surfaces.
Scientific applications and molecular chemistry
Beyond sports, the truncated icosahedron plays crucial roles in cutting-edge science:
Fullerene chemistry
The C60 molecule (Buckminsterfullerene or "Buckyball") follows this exact geometry, with 60 carbon atoms positioned at the vertices. This discovery revolutionized chemistry and materials science, leading to nanotechnology breakthroughs.
Virus architecture
Many virus capsids utilize icosahedral or truncated icosahedral structures for optimal packing of genetic material while maintaining structural integrity. This geometry provides maximum internal volume with minimal surface area.
Materials engineering
Engineers use truncated icosahedral principles in designing pressure vessels, architectural domes, and spacecraft components where strength, weight optimization, and uniform stress distribution are critical.
Computational modeling
In computer graphics and scientific simulation, this geometry serves as a fundamental primitive for creating spherical approximations and complex 3D models with manageable polygon counts.
Cultural impact and global recognition
No other polyhedron has achieved such universal cultural significance:
- Universal symbolism: Recognized across all cultures as the symbol of football/soccer
- Educational tool: Introduces millions of children to three-dimensional geometry
- Artistic inspiration: Featured in sculptures, architecture, and design worldwide
- Commercial applications: From toys to high-tech equipment design
- Scientific communication: Used to explain molecular structures and crystallography
- Space exploration: Model for satellite design and space station modules
- Environmental awareness: Symbol for global unity and cooperation
Manufacturing precision and engineering challenges
Panel fabrication
Creating perfect truncated icosahedra requires precise fabrication of 32 flat panels with exact edge lengths and angles. Modern soccer ball manufacturing uses computer-controlled cutting and thermal bonding to achieve geometric precision.
Pressure distribution
The geometry naturally distributes internal pressure evenly across all faces, making it ideal for inflatable applications. This uniform stress distribution prevents weak points and ensures structural integrity.
Quality control
Professional soccer balls undergo rigorous testing to ensure the truncated icosahedral geometry meets FIFA standards for circumference, weight, and sphericity. Advanced measurement systems verify geometric accuracy.
Modern innovations
While traditional panels remain popular, modern balls use thermally bonded segments and even spherical constructions, but the truncated icosahedral pattern remains the visual and conceptual standard.
Educational and philosophical significance
Mathematical gateway
For many people, the soccer ball provides their first encounter with complex three-dimensional geometry, Platonic and Archimedean solids, and the beauty of mathematical relationships in everyday objects.
STEM education
Teachers worldwide use soccer balls to demonstrate concepts in geometry, physics, chemistry, and engineering, making abstract mathematical principles tangible and relevant to students' lives.
Cross-cultural learning
The universal recognition of this geometric pattern creates opportunities for international collaboration in education and scientific research, transcending language and cultural barriers.
Philosophy of design
The soccer ball exemplifies how mathematical perfection can achieve practical functionality, aesthetic appeal, and cultural significance simultaneously, serving as a model for design thinking across disciplines.
Future applications and technological developments
Nanotechnology advances
Research into fullerene derivatives and carbon-based nanomaterials continues to explore variations of the truncated icosahedral structure for applications in electronics, medicine, and energy storage.
Space applications
The geometry's optimal strength-to-weight ratio makes it ideal for space-based structures, from satellite components to potential space habitat designs and interplanetary exploration equipment.
Sustainable design
Environmental architects and engineers are exploring truncated icosahedral principles for creating efficient, sustainable structures that minimize material use while maximizing functional space.
Virtual reality and gaming
In digital environments, this familiar geometry serves as a foundation for creating realistic physics simulations, interactive objects, and intuitive user interface elements that leverage users' existing familiarity.
Summary
The Truncated Icosahedron stands as the most successful bridge between pure mathematics and popular culture ever achieved. Through its transformation into the soccer ball, this ancient geometric form has touched more lives than any other mathematical object in human history. Its perfect balance of theoretical elegance and practical functionality demonstrates how mathematical principles can transcend academic boundaries to become integral parts of human culture, sport, science, and technology. From the molecular scale of fullerenes to the global scale of international sports, from ancient Greek geometry to cutting-edge nanotechnology, this remarkable polyhedron continues to inspire, educate, and unite people across all boundaries. As we advance into an increasingly complex technological future, the truncated icosahedron remains a perfect example of how mathematical beauty, practical utility, and cultural significance can combine to create objects that are simultaneously scientifically profound and universally beloved.