Truncated Octahedron Calculator
Calculator and formulas for calculating a truncated octahedron
Truncated Octahedron Calculator
The Truncated Octahedron
A Truncated Octahedron is the most elegant Archimedean solid with beautifully simple mathematical relationships.
Truncated Octahedron Structure
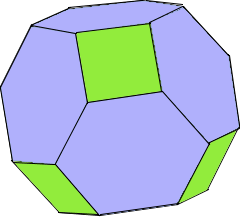
The most elegant and simple Archimedean solid.
Perfect balance: 6 squares and 8 hexagons.
|
|
What is a Truncated Octahedron?
A Truncated Octahedron is the most elegant and mathematically simple Archimedean solid:
- Definition: An octahedron with all 6 vertices truncated
- Faces: 6 squares + 8 hexagons (14 total)
- Elegance: Perfectly balanced and symmetric
- Vertices: 24 identical vertices
- Edges: 36 identical edges
- Simplicity: Beautiful mathematical relationships
Geometric Properties of the Truncated Octahedron
The Truncated Octahedron exhibits the most elegant geometric properties:
Basic Parameters
- Edge length (a): Length of all 36 identical edges
- Faces: Two types of regular polygons in perfect balance
- Euler characteristic: V - E + F = 24 - 36 + 14 = 2
- Dual form: Tetrakis hexahedron
Elegant Properties
- Perfect symmetry: Octahedral symmetry group
- Vertex figure: (4.6.6) - One square and two hexagons
- Simple formulas: Clean mathematical relationships
- Space-filling: Can tile 3D space perfectly
Mathematical Relationships
The Truncated Octahedron follows beautifully simple mathematical laws:
Volume Formula
Elegantly simple: just √2 coefficient. Factor 8√2 ≈ 11.31 creates beautiful proportions.
Surface Area
Perfect balance of squares and hexagons. Factor (1+2√3) ≈ 4.46 combines both face types.
Applications of the Truncated Octahedron
Truncated Octahedra are valuable in many fields due to their elegant simplicity:
Space-Filling Applications
- 3D space tiling and tessellation
- Efficient packing and storage systems
- Architectural modular construction
- Crystallographic unit cell structures
Materials Science
- Metal foam structures and lattices
- Molecular cage designs
- Honeycomb-like composite materials
- Optimal strength-to-weight structures
Engineering & Technology
- Heat exchanger and cooling systems
- Acoustic panels and sound dampening
- 3D printing support structures
- Robotics and mechanical design
Art & Design
- Architectural elements and facades
- Decorative patterns and motifs
- Sculpture and art installations
- Educational models and demonstrations
Formulas for the Truncated Octahedron
Volume V
Beautifully simple volume formula with √2
Surface S
Perfect balance of square and hexagonal areas
Outer radius rc
Simple circumradius with √10
Midsphere radius rm
Elegantly simple: just 3a/2
Edge length a (Inverse formulas)
from volume
from surface
from outer radius
from midsphere radius
Calculate edge length from other parameters
Face Area Analysis
Total area: 6a²
Total area: 12a²√3
Perfect balance: S = 6a² + 12a²√3 = 6a²(1+2√3)
Calculation Example for a Truncated Octahedron
Given
Find: All properties of the Elegant Truncated Octahedron
1. Volume Calculation
The volume is approximately 90.5 cubic units
2. Surface Calculation
The surface area is approximately 107 square units
3. Outer Radius
The outer radius is exactly √10 ≈ 3.16 units
4. Midsphere Radius
The midsphere radius is exactly 3.00 units
5. The Elegant Polyhedron
The most elegant Archimedean solid with beautifully simple mathematical relationships
The Truncated Octahedron: Elegance in Mathematical Simplicity
The Truncated Octahedron stands as the most elegant and mathematically beautiful of all Archimedean solids. While other uniform polyhedra dazzle with their complexity or cultural significance, the truncated octahedron achieves something perhaps even more remarkable: perfect mathematical simplicity combined with profound geometric utility. This extraordinary polyhedron represents the ideal balance between structural sophistication and mathematical elegance, demonstrating how the most beautiful forms often emerge from the simplest principles applied with perfect precision and harmony.
The essence of mathematical elegance
The Truncated Octahedron embodies mathematical elegance in its purest form:
- Perfect balance: 6 squares and 8 hexagons in ideal proportion
- Simple formulas: Clean mathematical relationships without complex nested radicals
- Rational coefficients: Many measurements involve simple fractions and basic square roots
- Space-filling property: Can perfectly tile three-dimensional space without gaps
- Octahedral symmetry: Inherits the beautiful 48-fold symmetry of its parent octahedron
- Vertex uniformity: Each vertex connects one square and two hexagons (4.6.6)
- Construction simplicity: Created by the most natural truncation of an octahedron
Historical recognition and mathematical appreciation
Ancient discovery
While Archimedes catalogued this solid over 2000 years ago, its mathematical elegance has made it a favorite of geometers throughout history. Its simple relationships and beautiful proportions have inspired mathematicians across cultures and centuries.
Renaissance appreciation
During the Renaissance, artists and mathematicians particularly admired its perfect balance of complexity and simplicity. Unlike more complex polyhedra, it could be constructed and understood without overwhelming mathematical machinery.
Modern relevance
In the modern era, its space-filling properties and structural efficiency have made it invaluable in materials science, architecture, and engineering applications where elegance meets functionality.
Educational ideal
Today, it serves as the perfect introduction to Archimedean solids, demonstrating complex geometric principles through beautifully simple mathematical relationships that students can understand and appreciate.
Mathematical beauty in simple formulas
The Truncated Octahedron showcases mathematical beauty through simplicity:
Volume elegance
The volume formula V = 8a³√2 is strikingly simple. The coefficient 8√2 ≈ 11.31 provides a clean relationship between edge length and volume, making calculations intuitive and memorable.
Surface simplicity
The surface area S = 6a²(1+2√3) beautifully separates the contributions of squares (6a²) and hexagons (12a²√3), making the geometric composition immediately clear and understandable.
Radius relationships
The midsphere radius rm = 3a/2 is remarkably simple - just a rational fraction! The circumradius rc = a√10/2 involves only √10, demonstrating the geometric clarity underlying this polyhedron.
Computational efficiency
Unlike complex polyhedra requiring nested radicals and golden ratio calculations, the truncated octahedron can be computed with basic arithmetic and simple square roots, making it computationally elegant.
Space-filling wonder and practical applications
The truncated octahedron's most remarkable property is its ability to fill space:
- Perfect tessellation: Can tile 3D space completely without gaps or overlaps
- Structural efficiency: Optimal strength-to-weight ratio in many applications
- Materials science: Template for foams, lattices, and composite structures
- Architecture: Modular construction systems and space-efficient designs
- Engineering: Heat exchangers, acoustic panels, and mechanical components
- Crystallography: Unit cell structures in various crystal systems
- Packaging design: Efficient space utilization and storage systems
Construction and manufacturing advantages
Construction simplicity
Unlike complex polyhedra requiring precision cuts at unusual angles, the truncated octahedron uses only squares and regular hexagons - shapes that are easy to fabricate accurately with standard tools and techniques.
Manufacturing efficiency
The two polygon types can be mass-produced using standard manufacturing processes, making large-scale construction economical and practical while maintaining geometric precision.
Assembly advantages
The regular patterns and simple vertex connections make assembly straightforward and error-resistant, reducing construction time and improving quality control in manufacturing applications.
Quality assurance
The simple geometric relationships make it easy to verify correctness during construction, with measurements and angles that can be checked using basic geometric principles and standard tools.
Aesthetic and philosophical significance
Perfect balance
The truncated octahedron represents perfect balance between simplicity and sophistication, demonstrating how mathematical elegance can be achieved without sacrificing geometric richness or structural utility.
Natural harmony
Its proportions and relationships feel natural and harmonious, creating forms that are both mathematically correct and aesthetically pleasing, appealing to both analytical and artistic sensibilities.
Educational inspiration
As an introduction to advanced geometry, it shows students how sophisticated three-dimensional relationships can emerge from simple principles, inspiring further mathematical exploration and appreciation.
Design philosophy
In design and engineering, it exemplifies the principle that the best solutions are often the simplest ones that meet all requirements - elegant, efficient, and beautiful simultaneously.
Contemporary applications and future potential
Advanced materials
Modern materials science increasingly utilizes truncated octahedral structures for creating lightweight, strong materials with optimal properties derived from the geometric efficiency of this elegant form.
Sustainable design
Its space-filling properties and material efficiency make it ideal for sustainable architecture and engineering, maximizing functionality while minimizing resource consumption and environmental impact.
Computational applications
In computational geometry and 3D modeling, its simple mathematical relationships make it efficient for algorithms and simulations, providing a perfect balance of geometric sophistication and computational efficiency.
Biomimetic potential
Nature often develops efficient structures, and the truncated octahedron's optimal properties make it a valuable template for biomimetic designs in materials, structures, and biological systems.
Summary
The Truncated Octahedron represents the pinnacle of mathematical elegance in three-dimensional geometry. Through its perfect balance of 6 squares and 8 hexagons, it achieves something remarkable: maximum geometric sophistication with minimum mathematical complexity. Its beautifully simple formulas, space-filling properties, and structural efficiency make it not just a mathematical curiosity but a practical tool for solving real-world problems in architecture, materials science, and engineering. From its ancient recognition by Archimedes to its modern applications in advanced materials and sustainable design, this elegant polyhedron continues to demonstrate that the most beautiful solutions are often the simplest ones. As we face increasingly complex challenges in technology and sustainability, the truncated octahedron serves as a reminder that elegance, efficiency, and beauty can coexist in perfect harmony, showing us that the most profound truths in mathematics are often expressed through the most beautiful simplicities.