Truncated Cube Calculator
Calculator and formulas for calculating a truncated cube
Truncated Cube Calculator
The Truncated Cube
A Truncated Cube is an Archimedean solid created by truncating a cube at its vertices.
Truncated Cube Structure
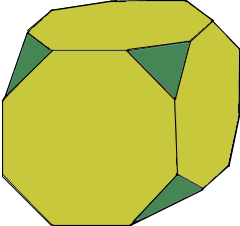
A Truncated Cube has regular octagonal and triangular faces.
It has 8 triangular and 6 octagonal faces.
|
|
What is a Truncated Cube?
A Truncated Cube is a classical Archimedean solid:
- Definition: A cube with all 8 vertices truncated
- Faces: 8 equilateral triangles + 6 regular octagons (14 total)
- Construction: Created by cutting off all corners of a cube
- Vertices: 24 identical vertices
- Edges: 36 identical edges
- Symmetry: Octahedral symmetry group
Geometric Properties of the Truncated Cube
The Truncated Cube possesses elegant geometric properties:
Basic Parameters
- Edge length (a): Length of all 36 edges
- Faces: 14 regular polygons (8 triangles + 6 octagons)
- Euler characteristic: V - E + F = 24 - 36 + 14 = 2
- Dual form: Triakis octahedron
Special Properties
- Archimedean solid: All vertices are congruent
- Vertex figure: (3.8.8) - One triangle and two octagons
- Octahedral symmetry: 48 symmetry operations
- Cube truncation: Created by truncating a cube
Mathematical Relationships
The Truncated Cube follows sophisticated mathematical laws:
Volume Formula
Complex volume involving √2. The factor (21+14√2)/3 ≈ 13.6 reflects truncation.
Surface Area
Combines triangular and octagonal areas. Both √2 and √3 appear in the formula.
Applications of the Truncated Cube
Truncated Cubes find applications in diverse fields:
Chemistry & Materials
- Molecular cage structures and fullerenes
- Crystal lattice structures and unit cells
- Coordination compounds with cubic symmetry
- Metal-organic framework materials
Architecture & Engineering
- Structural components and space frames
- Architectural elements with octagonal features
- Mechanical parts requiring specific geometry
- Industrial design and product development
Technology & Computing
- 3D modeling and computer graphics
- Mesh generation algorithms
- Computational geometry applications
- Virtual reality and gaming objects
Art & Design
- Sculptural works and installations
- Decorative objects and jewelry
- Educational geometric models
- Mathematical art and visualization
Formulas for the Truncated Cube
Volume V
Volume involving √2 from truncation geometry
Surface S
Surface combining triangular and octagonal areas
Height h
Height of the truncated cube
Outer radius rc
Circumradius with nested radical
Midsphere radius rm
Radius of sphere touching all edges
Edge length a (Inverse formulas)
from volume
from surface
from height
from outer radius
from midsphere radius
Calculate edge length from other parameters
Calculation Example for a Truncated Cube
Given
Find: All properties of the Truncated Cube
1. Volume Calculation
The volume is approximately 870 cubic units
2. Surface Calculation
The surface area is approximately 519 square units
3. Height Calculation
The height is approximately 9.66 units
4. Radii Calculations
Outer radius ≈ 6.93, Midsphere radius ≈ 6.83
5. Complete Truncated Cube
A classical Archimedean solid with all calculated properties
The Truncated Cube: Classical Elegance in Archimedean Geometry
The Truncated Cube stands as one of the most recognizable and historically significant Archimedean solids, representing the elegant transformation that occurs when the corners of a perfect cube are systematically removed. This classical polyhedron beautifully demonstrates how geometric truncation can create new forms of mathematical beauty while preserving underlying symmetries and introducing fascinating new relationships involving both triangular and octagonal faces.
Classical construction and cubic heritage
The Truncated Cube embodies the perfect balance between classical and innovative geometry:
- Cubic foundation: Built upon the most fundamental Platonic solid through systematic truncation
- Vertex truncation: Each of the 8 cube vertices is replaced by an equilateral triangle
- Face transformation: The 6 square faces become regular octagons through corner removal
- Edge uniformity: All 36 resulting edges have identical length, defining Archimedean character
- Octahedral symmetry: Inherits and preserves the symmetry group of the original cube
- Vertex configuration: Each vertex connects one triangle and two octagons (3.8.8)
Historical significance and mathematical development
Ancient origins
While Archimedes systematically studied this solid over 2000 years ago, evidence suggests that truncated cubes appeared in decorative arts and architecture even earlier, demonstrating humanity's intuitive appreciation for their aesthetic balance.
Medieval applications
Islamic mathematicians and artists incorporated truncated cubic forms into geometric patterns and architectural elements, recognizing their unique ability to combine angular and curved visual elements.
Renaissance mastery
During the Renaissance, artists like Dürer and mathematicians like Pacioli used truncated cubes to explore perspective, proportion, and the mathematical foundations of artistic beauty.
Modern relevance
Today, the truncated cube serves as a fundamental shape in crystallography, architecture, and design, where its combination of triangular and octagonal elements provides both structural and aesthetic advantages.
Mathematical sophistication and formula complexity
The truncated cube demonstrates remarkable mathematical depth:
Volume relationships
The volume formula V = a³(21+14√2)/3 elegantly combines rational coefficients with √2, reflecting the geometric relationship between the original cube and its truncated form. The factor (21+14√2)/3 ≈ 13.6 quantifies the volumetric effect of truncation.
Surface area complexity
The surface area S = 2a²(6+6√2+√3) beautifully incorporates both √2 (from octagonal geometry) and √3 (from triangular areas), demonstrating how different polygon types contribute to the total surface.
Radius formulas
The circumradius formula involving √(7+4√2) showcases nested radicals, while the midsphere radius with (2+√2) shows simpler but equally elegant relationships. These formulas reveal the deep mathematical structure underlying the truncation process.
Height relationships
The height h = a(1+√2) provides a direct connection between edge length and overall dimension, making the truncated cube particularly useful in practical applications requiring specific dimensional relationships.
Scientific and technological applications
The classical elegance of the truncated cube makes it valuable across many fields:
- Crystallography: Template for crystal structures with cubic symmetry and specific coordination numbers
- Materials science: Framework for designing materials with controlled porosity and surface properties
- Architecture: Building blocks for structures requiring both angular and octagonal elements
- Engineering design: Components in mechanical systems where cubic truncation provides optimal functionality
- Computer graphics: Fundamental primitive in 3D modeling software and game engines
- Chemistry: Molecular cage structures and coordination compounds with specific geometric requirements
- Educational tools: Perfect model for teaching geometric transformation and symmetry concepts
Construction techniques and practical considerations
Truncation precision
Creating a perfect truncated cube requires cutting each vertex at precisely the right depth to ensure edge uniformity. This precision requirement demonstrates the mathematical exactness underlying geometric beauty.
Manufacturing advantages
The combination of flat faces (triangles and octagons) makes truncated cubes relatively easy to manufacture while providing more surface complexity than simple cubes.
Dual relationships
Its dual, the triakis octahedron, has 24 triangular faces corresponding to the 24 vertices. This duality helps visualize the deep connections between different polyhedral families.
Packing properties
While not space-filling alone, truncated cubes can be combined with other shapes to create efficient packing arrangements, useful in materials design and space optimization.
Aesthetic and philosophical significance
Visual harmony
The truncated cube achieves perfect visual balance by combining the angular nature of triangles with the softer, more complex geometry of octagons, creating forms that are both dynamic and stable.
Symbolic meaning
In many cultures, the truncated cube represents the transformation of basic forms into more complex but harmonious structures, symbolizing growth, development, and the evolution of ideas.
Educational value
As one of the more accessible Archimedean solids, it provides an excellent introduction to concepts of truncation, vertex uniformity, and the relationship between different polygon types in three-dimensional space.
Design inspiration
Artists and designers continue to find inspiration in the truncated cube's perfect balance of regularity and complexity, using it as a foundation for both functional and decorative objects.
Summary
The Truncated Cube represents the perfect marriage of classical geometric principles and innovative mathematical thinking. Through the systematic truncation of a simple cube, we discover a polyhedron that maintains fundamental symmetries while introducing new levels of complexity and beauty. Its 14 faces, combining 8 triangular and 6 octagonal elements, create a structure that is both mathematically elegant and practically useful. From its ancient recognition by Archimedes to its modern applications in materials science and computer graphics, the truncated cube continues to demonstrate the enduring power of mathematical geometry to inspire, educate, and solve real-world problems. As we advance in our understanding of three-dimensional space and its applications, this classical Archimedean solid remains a testament to the timeless beauty that emerges when mathematical precision meets geometric imagination, proving that some of the most profound truths in mathematics are also the most beautiful.