Rhombicosidodecahedron Calculator
Calculator and formulas for calculating a rhombicosidodecahedron
Rhombicosidodecahedron Calculator
The Rhombicosidodecahedron
A Rhombicosidodecahedron is the most complex Archimedean solid with 62 faces of three different types.
Rhombicosidodecahedron Structure
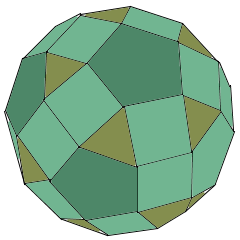
A Rhombicosidodecahedron is the most complex Archimedean solid.
It has 62 faces: 20 triangles, 30 squares, and 12 pentagons.
|
|
What is a Rhombicosidodecahedron?
A Rhombicosidodecahedron is the pinnacle of Archimedean complexity:
- Definition: Most complex semi-regular convex polyhedron
- Faces: 20 triangles + 30 squares + 12 pentagons (62 total)
- Complexity: Three different face types meeting at vertices
- Vertices: 60 identical vertices
- Edges: 120 identical edges
- Symmetry: Icosahedral symmetry group
Geometric Properties of the Rhombicosidodecahedron
The Rhombicosidodecahedron possesses the most complex geometric properties:
Basic Parameters
- Edge length (a): Length of all 120 edges
- Faces: 62 regular polygons (20+30+12)
- Euler characteristic: V - E + F = 60 - 120 + 62 = 2
- Dual form: Deltoidal hexecontahedron
Special Properties
- Archimedean solid: All vertices are congruent
- Vertex figure: (3.4.5.4) - Triangle, square, pentagon, square
- Icosahedral symmetry: 120 symmetry operations
- Maximum complexity: Most faces among Archimedean solids
Mathematical Relationships
The Rhombicosidodecahedron follows the most complex mathematical laws:
Volume Calculation
The most complex volume formula among Archimedean solids. Contains the golden ratio through √5.
Surface Calculation
Ultra-complex surface formula combining all three face types. Contains √3, √5, and nested radicals.
Applications of the Rhombicosidodecahedron
Rhombicosidodecahedra find applications in the most advanced fields:
Advanced Research
- Complex viral capsid architectures
- Large molecular cage compounds
- Sophisticated protein assemblies
- Advanced nanostructure design
Materials Science
- Complex quasicrystalline structures
- High-order coordination compounds
- Advanced metamaterial designs
- Sophisticated carbon cage molecules
Theoretical Mathematics
- Advanced group theory applications
- Complex symmetry operations
- Higher-dimensional geometry
- Topological complexity studies
Engineering Applications
- Ultra-complex architectural structures
- Advanced aerospace components
- Sophisticated artistic installations
- High-precision mechanical systems
Formulas for the Rhombicosidodecahedron
Volume V
Most complex volume formula among Archimedean solids
Surface S
Ultra-complex surface combining all three face types
Outer radius rc
Circumradius with nested golden ratio terms
Midsphere radius rm
Midsphere radius involving golden ratio
Edge length a (Inverse formulas)
from volume
from surface
from outer radius
from midsphere radius
Calculate edge length from other parameters
Calculation Example for a Rhombicosidodecahedron
Given
Find: All properties of the Rhombicosidodecahedron
1. Volume Calculation
The volume is approximately 1124 cubic units
2. Surface Calculation
The surface area is approximately 534 square units
3. Outer Radius
Outer radius is approximately 6.70
4. Midsphere Radius
Midsphere radius is approximately 6.53
5. Complete Rhombicosidodecahedron
The most complex Archimedean solid with all calculated properties
The Rhombicosidodecahedron: Pinnacle of Polyhedral Complexity
The Rhombicosidodecahedron represents the absolute pinnacle of Archimedean complexity and mathematical sophistication. As the most intricate semi-regular polyhedron, it embodies the ultimate expression of geometric harmony within the constraints of vertex-uniformity, showcasing how mathematical elegance can emerge from seemingly overwhelming complexity.
Definition and ultimate complexity
The Rhombicosidodecahedron stands as the most complex achievement in Archimedean geometry:
- Maximum complexity: 62 faces, 120 edges, and 60 vertices - the largest among all Archimedean solids
- Triple face types: 20 equilateral triangles, 30 squares, and 12 regular pentagons
- Vertex configuration: Each vertex connects triangle-square-pentagon-square (3.4.5.4)
- Golden ratio integration: Involves √5 and nested radical expressions
- Icosahedral symmetry: Possesses the highest possible rotational symmetry (120 operations)
- Dual polyhedron: Deltoidal hexecontahedron with 60 kite-shaped faces
Historical significance and mathematical achievement
Ancient aspirations
While the simpler Archimedean solids were known to ancient Greeks, the rhombicosidodecahedron represents the culmination of their geometric ambitions - a form so complex it challenged mathematical understanding for centuries.
Renaissance mastery
The complete understanding of this polyhedron required the mathematical sophistication of the Renaissance, when scholars like Kepler and Dürer could finally grasp its full geometric implications.
Modern applications
The 20th and 21st centuries have revealed applications in complex viral structures, advanced materials science, and sophisticated molecular architectures that require this level of geometric complexity.
Computational geometry
Modern computer graphics and CAD systems use the rhombicosidodecahedron as a benchmark for testing complex 3D algorithms and mesh generation techniques.
Construction and geometric relationships
Understanding the rhombicosidodecahedron requires sophisticated geometric thinking:
Complex truncation
It can be created through elaborate truncation processes applied to the icosidodecahedron, involving precise cuts that maintain the delicate balance between three different face types.
Golden ratio foundations
Its construction involves intricate relationships with the golden ratio, requiring nested calculations with √5 that reflect the underlying pentagonal symmetries.
Symmetry preservation
Despite its complexity, it maintains perfect icosahedral symmetry, demonstrating how mathematical order can persist through increasing geometric sophistication.
Topological complexity
The arrangement of 62 faces into a coherent whole represents one of the most challenging problems in polyhedral topology and construction geometry.
Advanced scientific applications
The extreme complexity makes it valuable in cutting-edge applications:
- Virology: Models for the most complex viral capsids with elaborate protein arrangements
- Supramolecular chemistry: Templates for designing enormous molecular cages and containers
- Nanotechnology: Blueprints for sophisticated nanostructures requiring maximum surface complexity
- Crystallography: Understanding the most complex quasicrystalline and aperiodic structures
- Architecture: Design principles for structures requiring maximum geometric sophistication
- Computer science: Benchmark problems for computational geometry and 3D algorithms
- Materials science: Design of metamaterials with complex surface properties
Mathematical formulas and computational challenges
Formula complexity
The volume formula V = a³(60+29√5)/3 and surface area S = a²(30+5√3+3√(25+10√5)) represent the most complex expressions in Archimedean geometry, involving multiple nested radicals and irrational constants.
Computational precision
Calculating properties requires high-precision arithmetic due to the accumulation of rounding errors in the complex radical expressions, making it a challenge for numerical analysis.
Symbolic mathematics
The formulas serve as excellent test cases for computer algebra systems, requiring sophisticated symbolic manipulation capabilities to handle the nested radical expressions accurately.
Geometric optimization
Its 62 faces create the most complex optimization problems in polyhedral geometry, relevant to surface area minimization and packing efficiency studies.
Philosophical and aesthetic significance
Complexity and order
The rhombicosidodecahedron demonstrates that mathematical beauty can emerge from extreme complexity, showing how order and elegance are not incompatible with sophistication.
Ultimate achievement
As the most complex Archimedean solid, it represents the ultimate achievement of vertex-uniform polyhedra, beyond which no greater complexity is possible within this classification.
Mathematical limits
It embodies the concept of mathematical limits - the boundary between achievable complexity and chaos, showing how structure can be maintained even at extremes.
Inspiration for innovation
Its existence inspires scientists and engineers to tackle increasingly complex problems, proving that sophisticated mathematical structures can be both understood and applied.
Summary
The Rhombicosidodecahedron stands as the ultimate testament to mathematical sophistication within the realm of semi-regular polyhedra. Its 62 faces, 120 edges, and 60 vertices create a structure of unparalleled complexity that nonetheless maintains perfect geometric order through icosahedral symmetry. The intricate formulas involving nested radicals and golden ratio relationships push the boundaries of computational geometry while providing blueprints for the most advanced applications in science and technology. From the most complex viral architectures to cutting-edge nanomaterials, from sophisticated mathematical algorithms to inspirational artistic creations, this extraordinary polyhedron proves that there are no limits to mathematical beauty and utility. As we continue to explore increasingly complex systems in science and engineering, the rhombicosidodecahedron remains our guide to understanding how ultimate complexity and perfect order can coexist in mathematical harmony.