Rhombicuboctahedron Calculator

Calculator and formulas for calculating a rhombicuboctahedron

Rhombicuboctahedron Calculator

The Rhombicuboctahedron

A Rhombicuboctahedron is an Archimedean solid with octagonal cross-sections and cubic symmetry.

Enter Known Parameter
Which parameter is known?
Value of the selected parameter
Rhombicuboctahedron Properties

Cubic Symmetry Polyhedron: Features octagonal cross-sections

26 Faces 48 Edges 24 Vertices 8 Triangles + 18 Squares
Rhombicuboctahedron Calculation Results
Edge length a:
Volume V:
Surface S:
Outer radius rc:
Midsphere radius rm:

Rhombicuboctahedron Structure

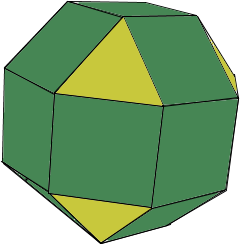
Rhombicuboctahedron

A Rhombicuboctahedron has octagonal cross-sections.
It consists of 8 equilateral triangles and 18 squares.

What is a Rhombicuboctahedron?

A Rhombicuboctahedron is a fascinating Archimedean solid:

  • Definition: Semi-regular convex polyhedron with 26 faces
  • Faces: 8 equilateral triangles + 18 squares
  • Cross-section: Regular octagon when viewed perpendicular to a square
  • Vertices: 24 identical vertices
  • Edges: 48 identical edges
  • Symmetry: Octahedral symmetry group

Geometric Properties of the Rhombicuboctahedron

The Rhombicuboctahedron possesses elegant geometric properties:

Basic Parameters
  • Edge length (a): Length of all 48 edges
  • Faces: 26 regular polygons (8 triangles + 18 squares)
  • Euler characteristic: V - E + F = 24 - 48 + 26 = 2
  • Dual form: Deltoidal icositetrahedron
Special Properties
  • Archimedean solid: All vertices are congruent
  • Vertex figure: (3.4.4.4) - One triangle and three squares
  • Octahedral symmetry: 48 symmetry operations
  • Truncation: Result of truncating a cuboctahedron

Mathematical Relationships

The Rhombicuboctahedron follows precise mathematical laws:

Volume Calculation
V = 2a³(6+5√2)/3

The volume grows cubically with edge length. The factor (6+5√2) ≈ 13.07 incorporates √2.

Surface Calculation
S = 2a²(9+√3)

The surface considers triangular and square faces. √3 comes from equilateral triangles.

Applications of the Rhombicuboctahedron

Rhombicuboctahedra find applications in various fields:

Crystallography & Chemistry
  • Crystal structures and coordination geometry
  • Molecular cage compounds and clusters
  • Coordination complexes with cubic symmetry
  • Metal framework structures
Architecture & Engineering
  • Space frame structures and trusses
  • Architectural elements with octagonal symmetry
  • Structural optimization designs
  • Mechanical components and joints
Mathematics & Computing
  • Computational geometry algorithms
  • 3D modeling and mesh generation
  • Symmetry group theory applications
  • Geometric optimization problems
Design & Games
  • Geometric puzzles and brain teasers
  • Educational models for stereometry
  • Artistic sculptures and installations
  • Game dice and probability applications

Formulas for the Rhombicuboctahedron

Volume V
\[V = \frac{2a^3 \cdot (6+5\sqrt{2})}{3}\]

Volume as a function of edge length a

Surface S
\[S = 2a^2 \cdot (9+\sqrt{3})\]

Total surface area of all 26 faces

Outer radius rc
\[r_c = \frac{a \cdot \sqrt{5+2\sqrt{2}}}{2}\]

Radius of the circumscribed sphere

Midsphere radius rm
\[r_m = \frac{a \cdot \sqrt{4+2\sqrt{2}}}{2}\]

Radius of the sphere touching all edges

Edge length a (Inverse formulas)
\[a = \sqrt[3]{\frac{3V}{2(6+5\sqrt{2})}}\]

from volume

\[a = \sqrt{\frac{S}{2(9+\sqrt{3})}}\]

from surface

\[a = \frac{2r_c}{\sqrt{5+2\sqrt{2}}}\]

from outer radius

\[a = \frac{2r_m}{\sqrt{4+2\sqrt{2}}}\]

from midsphere radius

Calculate edge length from other parameters

Calculation Example for a Rhombicuboctahedron

Given
Edge length a = 5

Find: All properties of the Rhombicuboctahedron

1. Volume Calculation
\[V = \frac{2 \times 5^3 \times (6+5\sqrt{2})}{3}\] \[V = \frac{2 \times 125 \times (6+7.07)}{3}\] \[V = \frac{250 \times 13.07}{3}\] \[V = 1089.2\]

The volume is approximately 1089 cubic units

2. Surface Calculation
\[S = 2 \times 5^2 \times (9+\sqrt{3})\] \[S = 2 \times 25 \times (9+1.732)\] \[S = 50 \times 10.732\] \[S = 536.6\]

The surface area is approximately 537 square units

3. Outer Radius
\[r_c = \frac{5 \times \sqrt{5+2\sqrt{2}}}{2}\] \[r_c = \frac{5 \times \sqrt{7.828}}{2}\] \[r_c = \frac{5 \times 2.798}{2}\] \[r_c = 6.995\]

Outer radius is approximately 7.00

4. Midsphere Radius
\[r_m = \frac{5 \times \sqrt{4+2\sqrt{2}}}{2}\] \[r_m = \frac{5 \times \sqrt{6.828}}{2}\] \[r_m = \frac{5 \times 2.613}{2}\] \[r_m = 6.53\]

Midsphere radius is approximately 6.53

5. Complete Rhombicuboctahedron
Edge length a = 5.00 Volume V = 1089.2
Surface S = 536.6 Outer radius rc = 7.00
Midsphere radius rm = 6.53 Octagonal cross-section

A perfect Archimedean solid with octahedral symmetry

The Rhombicuboctahedron: Octagonal Elegance in Three Dimensions

The Rhombicuboctahedron represents a perfect fusion of cubic and octahedral geometries, creating one of the most visually striking and mathematically elegant Archimedean solids. Its unique property of exhibiting regular octagonal cross-sections makes it a bridge between two-dimensional and three-dimensional geometric understanding.

Definition and octagonal characteristics

The Rhombicuboctahedron is distinguished by its remarkable geometric properties:

  • Face composition: 26 faces consisting of 8 equilateral triangles and 18 squares
  • Octagonal cross-sections: When viewed perpendicular to any square face, it displays a perfect regular octagon
  • Vertex configuration: Each of the 24 vertices connects one triangle and three squares (3.4.4.4)
  • Octahedral symmetry: Possesses the same symmetry group as the octahedron and cube
  • Truncation origin: Can be constructed by truncating a cuboctahedron at its vertices
  • Dual polyhedron: Deltoidal icositetrahedron with 24 kite-shaped faces

Historical development and mathematical recognition

Ancient foundations

While the basic concept was understood by ancient geometers, the rhombicuboctahedron's full properties were not systematically studied until the medieval period, when Islamic mathematicians explored truncation processes.

Renaissance precision

Dürer and other Renaissance artists incorporated rhombicuboctahedral forms into their architectural and artistic works, recognizing the aesthetic appeal of its octagonal projections.

Modern applications

The 19th and 20th centuries saw applications in crystallography, where its octahedral symmetry corresponds to important crystal systems found in nature.

Contemporary relevance

Today, it finds applications in architectural design, structural engineering, and computer graphics, where its regular octagonal projections are particularly useful.

Construction and geometric relationships

The rhombicuboctahedron can be understood through several geometric perspectives:

Truncation method

Starting with a cuboctahedron and truncating its vertices creates the rhombicuboctahedron. This process transforms the original vertices into square faces while preserving the triangular faces.

Octagonal projections

The most distinctive feature is its regular octagonal cross-sections. When sliced perpendicular to any square face, the resulting cross-section is always a regular octagon.

Symmetry preservation

Despite the truncation process, it maintains full octahedral symmetry, demonstrating how complex operations can preserve fundamental symmetry properties.

Dual relationships

Its dual, the deltoidal icositetrahedron, has 24 faces corresponding to the 24 vertices of the rhombicuboctahedron, illustrating the elegant duality in polyhedron theory.

Scientific and practical applications

The unique properties make it valuable in diverse applications:

  • Crystallography: Models crystal structures with octahedral symmetry, particularly in metal oxides and fluorides
  • Architecture: Design of buildings and structures requiring octagonal symmetry elements
  • Engineering: Structural components where octagonal cross-sections provide optimal strength-to-weight ratios
  • Computer graphics: 3D modeling where octagonal projections simplify rendering algorithms
  • Materials science: Templates for creating materials with specific octahedral coordination environments
  • Game design: Unusual dice and game pieces with octagonal symmetry properties
  • Art and sculpture: Aesthetic objects that utilize the appealing octagonal projections

Mathematical formulas and √2 relationships

√2 in volume formula

The volume formula V = 2a³(6+5√2)/3 prominently features √2, reflecting the fundamental role of this constant in octahedral and cubic geometries.

Surface area elegance

The surface area S = 2a²(9+√3) combines integer coefficients with √3, elegantly balancing the contributions of square and triangular faces.

Radius relationships

Both radius formulas involve √2 in nested radical expressions, showing how the octahedral symmetry permeates all geometric relationships.

Computational aspects

The formulas require careful handling of radical expressions, making them excellent test cases for symbolic computation and numerical analysis systems.

Octagonal geometry and visual appeal

Aesthetic harmony

The regular octagonal cross-sections create visually pleasing forms that have been appreciated by artists and designers throughout history. The octagon's eight-fold symmetry creates balanced, harmonious compositions.

Structural efficiency

Octagonal cross-sections provide excellent structural properties, combining the strength advantages of circular forms with the manufacturing convenience of polygonal shapes.

Visualization benefits

The octagonal projections make the rhombicuboctahedron particularly useful in technical drawing and engineering applications where clear, recognizable cross-sections are important.

Pedagogical value

Its clear relationship between 3D form and 2D projections makes it an excellent educational tool for teaching spatial geometry and cross-sectional analysis.

Summary

The Rhombicuboctahedron stands as a testament to the beautiful interplay between two-dimensional and three-dimensional geometry. Its unique property of exhibiting regular octagonal cross-sections when viewed from specific angles makes it both mathematically fascinating and practically useful. The elegant formulas involving √2 and √3 reflect its deep connections to fundamental geometric constants, while its 26 faces create a complex yet harmonious structure that has inspired architects, artists, and engineers for centuries. From crystal structures to architectural designs, from computer graphics to structural engineering, the rhombicuboctahedron continues to demonstrate how mathematical beauty and practical utility can be perfectly aligned. As we advance in our understanding of three-dimensional space and its applications, this remarkable polyhedron remains a cornerstone of geometric thinking, bridging the gap between abstract mathematical theory and tangible real-world applications.

Cuboctahedron • Icosidodecahedron • Rhombicosidodecahedron • Rhombicuboctahedron • Snub cube • Truncated cube • Snub dodecahedron • Truncated cuboctahedron • Truncated dodecahedron • Truncated icosahedron • Truncated icosidodecahedron • Truncated octahedron • Truncated tetrahedron