Truncated Tetrahedron Calculator
Calculator and formulas for calculating a truncated tetrahedron
Truncated Tetrahedron Calculator
The Truncated Tetrahedron
A Truncated Tetrahedron is the simplest Archimedean solid with tetrahedral symmetry and uniform edges.
Truncated Tetrahedron Structure
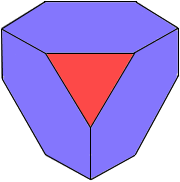
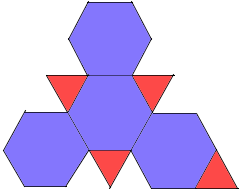
A Truncated Tetrahedron is the simplest Archimedean solid.
It has 4 triangular and 4 hexagonal faces.
|
|
What is a Truncated Tetrahedron?
A Truncated Tetrahedron is the simplest and most fundamental Archimedean solid:
- Definition: A tetrahedron with corners cut off to create uniform edge lengths
- Faces: 4 equilateral triangles + 4 regular hexagons (8 total)
- Construction: Created by truncating a regular tetrahedron at each vertex
- Vertices: 12 identical vertices
- Edges: 18 identical edges
- Symmetry: Tetrahedral symmetry group
Geometric Properties of the Truncated Tetrahedron
The Truncated Tetrahedron possesses elegant geometric properties:
Basic Parameters
- Edge length (a): Length of all 18 edges
- Faces: 8 regular polygons (4 triangles + 4 hexagons)
- Euler characteristic: V - E + F = 12 - 18 + 8 = 2
- Dual form: Triakis tetrahedron
Special Properties
- Archimedean solid: All vertices are congruent
- Vertex figure: (3.6.6) - One triangle and two hexagons
- Tetrahedral symmetry: 12 symmetry operations
- Simplest truncation: First in the Archimedean series
Mathematical Relationships
The Truncated Tetrahedron follows elegant mathematical laws:
Volume Calculation
The volume grows cubically with edge length. The factor 23√2/12 ≈ 2.71 is characteristic.
Surface Calculation
Simple surface area formula involving √3. Combines triangular and hexagonal face areas.
Applications of the Truncated Tetrahedron
Truncated Tetrahedra find applications in fundamental areas:
Chemistry & Materials
- Molecular cage structures and clusters
- Coordination compounds with tetrahedral geometry
- Crystal structures and unit cells
- Catalytic framework materials
Engineering & Design
- Structural elements and joints
- Architectural components
- Mechanical parts with tetrahedral symmetry
- Space frame structures
Mathematics & Computing
- Computational geometry algorithms
- 3D modeling and mesh generation
- Symmetry group theory studies
- Educational geometry models
Games & Art
- Geometric puzzles and games
- Artistic sculptures and installations
- Educational polyhedron models
- Decorative geometric objects
Formulas for the Truncated Tetrahedron
Volume V
Volume as a function of edge length a
Surface S
Total surface area of all 8 faces
Outer radius rc
Radius of the circumscribed sphere
Midsphere radius rm
Radius of the sphere touching all edges
Edge length a (Inverse formulas)
from volume
from surface
from outer radius
from midsphere radius
Calculate edge length from other parameters
Calculation Example for a Truncated Tetrahedron
Given
Find: All properties of the Truncated Tetrahedron
1. Volume Calculation
The volume is approximately 585 cubic units
2. Surface Calculation
The surface area is approximately 437 square units
3. Outer Radius
Outer radius is approximately 7.04
4. Midsphere Radius
Midsphere radius is approximately 6.36
5. Complete Truncated Tetrahedron
The simplest Archimedean solid with all calculated properties
The Truncated Tetrahedron: Foundation of Archimedean Geometry
The Truncated Tetrahedron holds a special place in polyhedral geometry as the simplest and most fundamental of all Archimedean solids. By truncating the corners of a regular tetrahedron—the simplest of all Platonic solids—we create the first semi-regular polyhedron, establishing the foundation for understanding how complex geometric structures can emerge from simple, systematic operations.
Fundamental geometric construction
The Truncated Tetrahedron exemplifies the elegance of geometric transformation:
- Truncation process: Created by cutting off the corners of a regular tetrahedron at a specific depth
- Edge uniformity: All 18 edges become equal in length, a defining characteristic of Archimedean solids
- Face composition: 4 equilateral triangles (reduced from original faces) and 4 regular hexagons (new faces)
- Vertex configuration: Each vertex connects one triangle and two hexagons (3.6.6)
- Tetrahedral symmetry: Maintains the symmetry group of the original tetrahedron
- Euler's formula: Satisfies V - E + F = 12 - 18 + 8 = 2
Historical significance and mathematical development
Ancient foundations
While Archimedes studied this solid over 2000 years ago, the truncated tetrahedron represents humanity's first systematic exploration beyond the five Platonic solids, opening the door to semi-regular geometry.
Renaissance rediscovery
Renaissance mathematicians like Dürer and Pacioli used the truncated tetrahedron to understand the principles of truncation that would later be applied to create the entire family of Archimedean solids.
Modern applications
Today, the truncated tetrahedron serves as a fundamental building block in chemistry, materials science, and engineering, where its simple yet elegant structure provides optimal balance between complexity and practicality.
Educational importance
As the simplest Archimedean solid, it serves as the perfect introduction to semi-regular polyhedra in mathematics education, helping students understand vertex uniformity and geometric transformation.
Mathematical elegance and formula simplicity
The truncated tetrahedron demonstrates mathematical beauty through simplicity:
Volume relationships
The volume formula V = 23a³√2/12 elegantly combines the factor 23/12 (representing the truncation effect) with √2 (reflecting the tetrahedral geometry), creating a bridge between Platonic and Archimedean mathematics.
Surface area harmony
The surface area S = 7a²√3 beautifully incorporates the factor 7 (representing the total face contribution) with √3 (from both triangular and hexagonal geometries), unifying different polygon types in a single expression.
Radius calculations
The radius formulas involving √22 and √2 show how the truncation affects the polyhedron's three-dimensional properties, creating new geometric relationships not found in the original tetrahedron.
Computational accessibility
Unlike more complex Archimedean solids, the truncated tetrahedron's formulas are computationally straightforward, making it ideal for educational purposes and practical applications.
Scientific and technological applications
The fundamental nature of the truncated tetrahedron makes it valuable across many fields:
- Molecular chemistry: Framework for tetrahedral coordination compounds and cage molecules
- Crystallography: Basic structural unit in crystal lattices and space-filling arrangements
- Materials science: Template for creating materials with controlled porosity and surface properties
- Engineering design: Structural elements in space frames and architectural applications
- Computer graphics: Fundamental shape in 3D modeling and mesh generation algorithms
- Game theory: Fair dice and probability applications requiring multiple face types
- Educational tools: Physical models for teaching geometry and spatial reasoning
Construction techniques and practical considerations
Truncation precision
Creating a perfect truncated tetrahedron requires cutting each corner at exactly the right depth to ensure all edges become equal. This precision requirement illustrates the mathematical exactness underlying geometric beauty.
Manufacturing advantages
The relatively simple geometry makes truncated tetrahedra easier to manufacture than more complex Archimedean solids, while still providing the benefits of semi-regular structure.
Dual relationships
Its dual, the triakis tetrahedron, has 12 triangular faces corresponding to the 12 vertices. This duality relationship helps understand the deep connections in polyhedral geometry.
Space-filling properties
While not space-filling by itself, truncated tetrahedra can be combined with other shapes to create efficient packing arrangements, useful in materials design and architecture.
Philosophical and aesthetic significance
Gateway to complexity
The truncated tetrahedron represents humanity's first step beyond the classical Platonic solids, showing how simple operations can create new forms of mathematical beauty and utility.
Balance and proportion
Its combination of triangular and hexagonal faces creates a visual harmony that has inspired artists and designers, demonstrating how mathematical principles can enhance aesthetic appeal.
Educational foundation
As the simplest Archimedean solid, it provides the perfect introduction to advanced geometric concepts, helping students transition from basic to sophisticated mathematical thinking.
Symbolic significance
The truncated tetrahedron symbolizes the power of mathematical transformation—showing how systematic modification of simple forms can create entirely new geometric possibilities.
Summary
The Truncated Tetrahedron stands as the cornerstone of Archimedean geometry, representing the elegant simplicity that underlies all semi-regular polyhedra. Through the systematic truncation of a regular tetrahedron, we discover how mathematical operations can transform simple forms into more complex yet equally beautiful structures. Its 8 faces, combining triangular and hexagonal geometries in perfect harmony, demonstrate the fundamental principles that govern vertex uniformity and edge equality. From its role in molecular chemistry to its applications in modern engineering, from its historical significance to its educational value, the truncated tetrahedron continues to serve as our gateway to understanding the profound beauty and practical utility of mathematical geometry. As the simplest member of the Archimedean family, it reminds us that complexity often begins with elegant simplicity, and that the most fundamental mathematical truths can be both beautiful and endlessly useful.