Truncated Dodecahedron Calculator
Calculator and formulas for calculating a truncated dodecahedron
Truncated Dodecahedron Calculator
The Truncated Dodecahedron
A Truncated Dodecahedron is an Archimedean solid created by truncating a dodecahedron at its vertices.
Truncated Dodecahedron Structure
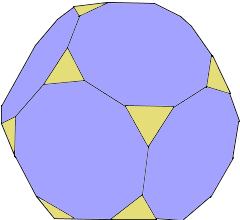
A Truncated Dodecahedron has triangular and decagonal faces.
It has 20 triangles and 12 regular decagons.
|
|
What is a Truncated Dodecahedron?
A Truncated Dodecahedron is a magnificent Archimedean solid:
- Definition: A dodecahedron with all 20 vertices truncated
- Faces: 20 equilateral triangles + 12 regular decagons (32 total)
- Construction: Created by cutting off all corners of a dodecahedron
- Vertices: 60 identical vertices
- Edges: 90 identical edges
- Golden ratio: Contains pentagonal symmetry and φ (phi)
Geometric Properties of the Truncated Dodecahedron
The Truncated Dodecahedron exhibits remarkable pentagonal geometry:
Basic Parameters
- Edge length (a): Length of all 90 identical edges
- Faces: 32 regular polygons (triangles and decagons)
- Euler characteristic: V - E + F = 60 - 90 + 32 = 2
- Dual form: Pentakis icosidodecahedron
Special Properties
- Archimedean solid: All vertices are congruent
- Vertex figure: (3.10.10) - One triangle and two decagons
- Icosahedral symmetry: 120 symmetry operations
- Golden ratio relation: Contains φ = (1+√5)/2
Mathematical Relationships
The Truncated Dodecahedron follows elegant mathematical laws involving the golden ratio:
Volume Formula
Complex volume involving √5 (golden ratio). Factor contains 99+47√5 ≈ 204 from pentagonal geometry.
Surface Area
Combines triangular and decagonal areas. Nested radicals involving golden ratio appear.
Applications of the Truncated Dodecahedron
Truncated Dodecahedra find applications in diverse fields involving pentagonal symmetry:
Chemistry & Biology
- Fullerene cage structures and carbon allotropes
- Virus capsid architectures with icosahedral symmetry
- Molecular self-assembly with golden ratio
- Quasicrystal structures and pentagonal tilings
Sports & Recreation
- Soccer ball design (classic black and white pattern)
- Geodesic dome construction principles
- Sports equipment with optimal aerodynamics
- Recreational puzzles and gaming dice
Architecture & Design
- Geodesic domes and spherical structures
- Architectural elements with pentagonal motifs
- Decorative panels and ceiling designs
- Sustainable building forms and eco-architecture
Mathematics & Education
- Golden ratio and pentagonal symmetry studies
- Advanced geometry and crystallography
- Computer graphics and 3D modeling
- Mathematical art and visualization tools
Formulas for the Truncated Dodecahedron
Volume V
Volume with golden ratio √5 coefficient
Surface S
Surface with nested radicals and golden ratio
Outer radius rc
Circumradius with golden ratio term
Midsphere radius rm
Radius involving golden ratio √5
Edge length a (Inverse formulas)
from volume
from surface
from outer radius
from midsphere radius
Calculate edge length from other parameters
Golden Ratio φ (Phi)
The golden ratio appears throughout pentagonal geometry
Calculation Example for a Truncated Dodecahedron
Given
Find: All properties of the Truncated Dodecahedron
1. Volume Calculation
The volume is approximately 680 cubic units
2. Surface Calculation
The surface area is approximately 358 square units
3. Outer Radius
The outer radius is approximately 5.94 units
4. Midsphere Radius
The midsphere radius is approximately 5.85 units
5. Complete Truncated Dodecahedron
A magnificent Archimedean solid with pentagonal symmetry and golden ratio proportions
The Truncated Dodecahedron: Sacred Geometry and Golden Ratio
The Truncated Dodecahedron stands as one of the most magnificent and culturally significant polyhedra in all of mathematics. This extraordinary Archimedean solid embodies the perfect marriage of pentagonal symmetry and the golden ratio, creating a form that has captivated mathematicians, artists, architects, and philosophers for millennia. Most famously recognized as the pattern of a classic soccer ball, it represents far more than a simple geometric construction - it is a gateway to understanding some of the deepest mathematical relationships in nature and a testament to the universal principles of beauty and proportion.
The soccer ball connection and cultural impact
The Truncated Dodecahedron's most visible manifestation is the classic soccer ball:
- Iconic design: The familiar black and white pattern with 12 pentagonal and 20 hexagonal patches
- Note: Traditional soccer balls use a truncated icosahedron, but the truncated dodecahedron represents the "inverse" pattern
- Optimal sphericity: The 32-face structure provides excellent approximation to a sphere
- Historical significance: First used in soccer balls in the 1970 FIFA World Cup
- Global recognition: Instantly recognizable worldwide as a symbol of sport and unity
- Mathematical education: Introduction point for millions to polyhedra and geometry
Golden ratio and pentagonal mystique
The golden ratio φ
φ = (1+√5)/2 ≈ 1.618... appears throughout the geometry. This divine proportion, known to the ancient Greeks, governs the relationships between pentagonal elements and creates the harmonic proportions that make this solid so aesthetically pleasing.
Pentagonal symmetry
Based on the dodecahedron with its 12 pentagonal faces, this solid inherits all the mystical and mathematical properties of five-fold symmetry. Pentagon patterns appear in flowers, fruits, and many biological structures.
Sacred geometry traditions
Throughout history, pentagonal forms have been associated with life, growth, and harmony. The truncated dodecahedron embodies these principles in three-dimensional perfection, making it a powerful symbol in sacred geometry.
Fibonacci connections
The golden ratio's appearance connects this polyhedron to the Fibonacci sequence, spiral patterns in nature, and the mathematical principles underlying organic growth and form.
Complex mathematical relationships
The truncated dodecahedron showcases sophisticated mathematical beauty:
Volume complexity
The volume formula V = 5a³(99+47√5)/12 elegantly combines rational and irrational terms. The coefficient (99+47√5) ≈ 204 reflects the intricate geometry created by truncating pentagonal vertices.
Surface area sophistication
The surface area S = 5a²(√3+6√(5+2√5)) is one of the most complex among Archimedean solids, involving nested radicals and multiple square root terms that reflect the geometric complexity of combining triangular and decagonal faces.
Radius formulations
Both circumradius and midsphere radius formulas involve √5 terms directly related to the golden ratio, demonstrating how pentagonal geometry naturally incorporates this fundamental mathematical constant.
Icosahedral symmetry
With 120 symmetry operations, this solid belongs to the icosahedral symmetry group, the richest and most complex of the platonic symmetries, connecting it to the deepest principles of three-dimensional order.
Scientific and natural applications
The truncated dodecahedron appears throughout nature and science:
- Virus architecture: Many virus capsids use icosahedral symmetry principles related to this geometry
- Fullerene chemistry: Carbon cage molecules often exhibit related pentagonal-hexagonal patterns
- Crystallography: Quasicrystals with pentagonal symmetry challenge traditional crystallographic principles
- Geodesic engineering: Dome structures based on these principles provide optimal strength-to-weight ratios
- Biological structures: Pollen grains, radiolaria, and other organisms exhibit similar geometric patterns
- Astronomical objects: Some planetarium projections and celestial mappings use related geometries
- Materials science: Advanced materials with designed pentagonal symmetries for unique properties
Construction and manufacturing considerations
Precise truncation
Creating a perfect truncated dodecahedron requires extremely precise truncation of the dodecahedron's vertices. Each cut must be exactly positioned to ensure all resulting edges have identical length while maintaining the correct face angles.
Manufacturing challenges
The combination of triangular and decagonal faces creates significant manufacturing complexity. Tooling must accommodate two different polygon types while maintaining perfect edge alignment and face planarity.
Sports equipment applications
While most soccer balls actually use the truncated icosahedron pattern, the principles and manufacturing techniques developed for these complex polyhedra have revolutionized sports equipment design and production.
Quality control requirements
The 32 faces and 90 edges require sophisticated quality control systems to ensure geometric accuracy. Modern manufacturing uses coordinate measuring machines and computer-controlled inspection systems.
Philosophical and aesthetic significance
Universal harmony
The truncated dodecahedron represents the harmony between different geometric principles - the stability of triangles, the perfection of pentagons and decagons, and the unity of the whole. This makes it a powerful symbol of universal harmony and mathematical beauty.
Artistic inspiration
Artists throughout history have been drawn to its complex beauty. From Renaissance studies of regular solids to contemporary sculptural works, it continues to inspire creative expression at the intersection of art and mathematics.
Educational value
As a bridge between simple geometric concepts and advanced mathematical principles, it provides an ideal educational tool for exploring symmetry, the golden ratio, and the relationship between mathematics and nature.
Cultural symbolism
In many cultures, the pentagonal symmetry and golden ratio proportions of this solid represent life, growth, and divine proportion, making it a recurring motif in spiritual and philosophical traditions.
Contemporary relevance and future directions
Advanced materials
Research into materials with truncated dodecahedral structures is revealing new possibilities for metamaterials with unique mechanical, optical, and acoustic properties derived from their complex geometric organization.
Nanotechnology applications
At the nanoscale, structures based on this geometry are being explored for drug delivery systems, molecular cages, and advanced catalyst supports that take advantage of its unique surface properties.
Computational modeling
Modern computational power allows for detailed analysis of structures based on truncated dodecahedral geometries, opening new applications in aerospace, automotive, and structural engineering.
Environmental applications
Its optimal surface-to-volume ratio and structural efficiency make it relevant for sustainable design applications, from efficient building structures to optimized packaging and container design.
Summary
The Truncated Dodecahedron represents the perfect confluence of mathematical elegance, natural beauty, and practical application. Through its intricate geometry involving the golden ratio and pentagonal symmetry, it connects us to some of the deepest principles underlying natural form and mathematical harmony. From its familiar appearance in sports equipment to its sophisticated applications in materials science and molecular chemistry, this remarkable polyhedron continues to reveal new facets of its significance. As both a mathematical object of extraordinary beauty and a practical form with countless applications, it serves as a bridge between the abstract world of mathematical ideals and the concrete realm of engineering and design. In an age of increasing technological complexity and environmental consciousness, the truncated dodecahedron's optimal properties and universal appeal make it more relevant than ever, continuing to inspire mathematicians, scientists, artists, and engineers in their quest to understand and harness the power of geometric perfection.