Cuboctahedron Calculator
Calculator and formulas for calculating a Cuboctahedron
Cuboctahedron Calculator
The Cuboctahedron
A Cuboctahedron is an Archimedean solid that represents the combination of a cube and an octahedron.
Cuboctahedron Structure
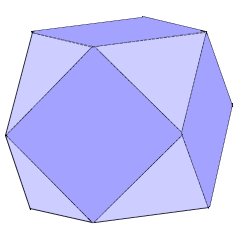
A Cuboctahedron combines cube and octahedron properties.
It consists of 8 equilateral triangles and 6 squares.
|
|
What is a Cuboctahedron?
A Cuboctahedron is a unique Archimedean solid:
- Definition: Semi-regular convex polyhedron
- Faces: 8 equilateral triangles + 6 squares
- Dual Nature: Represents the intersection of cube and octahedron
- Vertices: 12 identical vertices
- Edges: 24 identical edges
- Symmetry: Octahedral symmetry group
Geometric Properties of the Cuboctahedron
The Cuboctahedron possesses fascinating geometric properties:
Basic Parameters
- Edge length (a): Length of all 24 edges
- Faces: 14 regular polygons (8 triangles + 6 squares)
- Euler characteristic: V - E + F = 12 - 24 + 14 = 2
- Dual form: Rhombic dodecahedron
Special Properties
- Archimedean solid: All vertices are congruent
- Vertex figure: (3.4.3.4) - Alternating triangles and squares
- Octahedral symmetry: 48 symmetry operations
- Rectification: Result of truncating cube or octahedron midpoints
Mathematical Relationships
The Cuboctahedron follows precise mathematical laws:
Volume Calculation
The volume grows cubically with edge length. The factor 5√2/3 ≈ 2.36 is characteristic.
Surface Calculation
The surface considers triangular and square faces. √3 comes from equilateral triangles.
Applications of the Cuboctahedron
Cuboctahedra find applications in various fields:
Crystallography & Chemistry
- Crystal structures and lattice arrangements
- Coordination compounds and molecular geometry
- Packing structures in solid state chemistry
- Metal cluster compounds and cages
Architecture & Design
- Geodesic domes and space frame structures
- Modern sculptural architecture
- Modular construction systems
- Decorative elements and artistic installations
Mathematics & Computer Science
- Graph theory and network topology
- 3D computer graphics and modeling
- Finite element methods and mesh generation
- Symmetry groups and group theory
Games & Education
- Geometric puzzles and educational models
- Teaching aids for stereometry
- Unusual dice forms for strategy games
- Virtual reality and 3D visualization
Formulas for the Cuboctahedron
Volume V
Volume as a function of edge length a
Surface S
Total surface area of all 14 faces
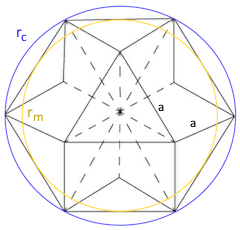
Outer radius rc
Radius of the circumscribed sphere
Midsphere radius rm
Radius of the sphere touching all edges
Edge length a (Inverse formulas)
from volume
from surface
from outer radius
from midsphere radius
Calculate edge length from other parameters
Calculation Example for a Cuboctahedron
Given
Find: All properties of the Cuboctahedron
1. Volume Calculation
The volume is approximately 509 cubic units
2. Surface Calculation
The surface area is approximately 341 square units
3. Outer Radius
Outer radius equals edge length: 6.00
4. Midsphere Radius
Midsphere radius is approximately 5.20
5. Complete Cuboctahedron
A perfect Archimedean solid with all calculated properties
The Cuboctahedron: Bridge Between Cube and Octahedron
The Cuboctahedron is one of the most symmetric and elegant Archimedean solids, representing a perfect balance between the cube and octahedron. This remarkable polyhedron embodies the mathematical concept of rectification and demonstrates the deep connections between different geometric forms.
Definition and fundamental properties
The Cuboctahedron is characterized by its unique position in polyhedron theory:
- Archimedean solid: Semi-regular convex polyhedron with identical vertices
- Dual nature: Can be seen as a truncated cube or truncated octahedron
- Face structure: 8 equilateral triangles and 6 squares (total 14 faces)
- Vertex configuration: Each vertex is surrounded by 2 triangles and 2 squares (3.4.3.4)
- Octahedral symmetry: Possesses the full symmetry group of the octahedron
- Rectification product: Result of truncating cube or octahedron at edge midpoints
Historical development and mathematical significance
Ancient origins
While named after Archimedes, the cuboctahedron was known to ancient mathematicians. It appears in the work of Plato and was studied by early geometers interested in regular and semi-regular polyhedra.
Renaissance rediscovery
Leonardo da Vinci drew cuboctahedra for Luca Pacioli's "De Divina Proportione" (1509). The Renaissance brought renewed interest in polyhedra and their artistic applications.
Modern crystallography
The 19th and 20th centuries revealed the cuboctahedron's importance in crystal structures, particularly in metal lattices and coordination compounds where it appears as a common coordination polyhedron.
Contemporary applications
Today, the cuboctahedron finds applications in nanotechnology, materials science, and architectural design as an optimal structural form with high symmetry and stability.
Construction and geometric relationships
The cuboctahedron can be constructed and understood through several methods:
Rectification process
The cuboctahedron is the rectification of both the cube and octahedron. By truncating these Platonic solids at their edge midpoints, the same cuboctahedron results - demonstrating the duality relationship.
Coordinate geometry
Vertices can be systematically placed at (±1,±1,0), (±1,0,±1), and (0,±1,±1), creating a highly symmetric arrangement in 3D space.
Related polyhedra
The cuboctahedron is central to a family of related forms including the truncated cube, truncated octahedron, and rhombicuboctahedron. It represents the "parent" form of many Archimedean solids.
Dual relationship
Its dual polyhedron is the rhombic dodecahedron, which has 12 rhombic faces. This duality relationship is fundamental in crystallography and materials science.
Scientific and technical applications
The practical importance of the cuboctahedron extends across many fields:
- Crystallography: Common coordination polyhedron in crystal structures, especially in metals
- Materials science: Optimal packing arrangements and nanoparticle geometries
- Chemistry: Molecular cage structures and coordination compounds
- Architecture: Space frame structures and geodesic constructions
- Computer graphics: 3D modeling and mesh generation algorithms
- Game theory: Fair dice design and probability applications
- Robotics: Optimal joint configurations and modular designs
Special mathematical properties
Numerical elegance
The volume formula V = (5√2/3)a³ ≈ 2.36a³ contains the fundamental constant √2, reflecting the deep connection to both cubic and octahedral geometry.
Surface optimization
The surface area formula S = 2a²(3+√3) elegantly combines the areas of triangular and square faces, with √3 arising from equilateral triangles.
Radius relationships
The remarkable property that rc = a (outer radius equals edge length) makes the cuboctahedron unique among Archimedean solids and simplifies many calculations.
Golden proportions
While not directly containing the golden ratio, the cuboctahedron's proportions relate to other important mathematical constants and harmonic relationships in geometry.
Physical and biological relevance
Optimal packing
The cuboctahedron plays a crucial role in optimal sphere packing problems and appears in the densest known arrangements of spheres in three dimensions.
Crystal physics
Many important crystal structures, including face-centered cubic (FCC) metals, can be understood through cuboctahedral coordination environments.
Biological structures
Viral capsids and protein assemblies sometimes adopt cuboctahedral symmetry, particularly in larger viral structures where high symmetry is advantageous.
Engineering applications
The high symmetry and structural stability make cuboctahedral forms ideal for aerospace applications, satellite design, and precision mechanical components.
Summary
The Cuboctahedron represents geometric harmony in its purest form, bridging the fundamental Platonic solids through the elegant process of rectification. Its unique properties - from the simple relationship rc = a to its role as the intersection of cube and octahedron - make it a cornerstone of three-dimensional geometry. The mathematical formulas involving √2 and √3 connect it to fundamental geometric constants, while its octahedral symmetry provides the highest possible regularity for a polyhedron with mixed face types. From ancient Greek mathematics to modern nanotechnology, from crystal structures to architectural marvels, the cuboctahedron continues to inspire and serve as a model of geometric perfection. As both a mathematical object of beauty and a practical tool for understanding three-dimensional space, it embodies the profound unity between theoretical elegance and real-world applications that defines the best of mathematical science.