Snub Dodecahedron Calculator

Calculator and formulas for calculating a snub dodecahedron

Snub Dodecahedron Calculator

The Snub Dodecahedron

A Snub Dodecahedron is the most complex chiral Archimedean solid with pentagonal and triangular faces.

Enter Known Parameter
Which parameter is known?
Value of the selected parameter
Snub Dodecahedron Properties

Most Complex Chiral Solid: The largest Archimedean solid with golden ratio relationships

92 Faces 150 Edges 60 Vertices 80 Triangles + 12 Pentagons
Snub Dodecahedron Calculation Results
Edge length a:
Volume V:
Surface S:
Outer radius rc:
Midsphere radius rm:

Snub Dodecahedron Structure

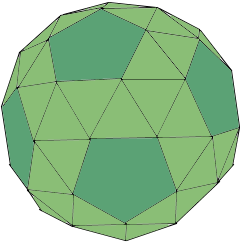
Snub Dodecahedron

A Snub Dodecahedron is the largest chiral Archimedean solid.
It has 80 equilateral triangles and 12 regular pentagons.

What is a Snub Dodecahedron?

A Snub Dodecahedron is the most complex chiral Archimedean solid:

  • Definition: The largest and most complex chiral Archimedean solid
  • Faces: 80 equilateral triangles + 12 regular pentagons (92 total)
  • Chirality: Exists in left-handed and right-handed forms
  • Vertices: 60 identical vertices
  • Edges: 150 identical edges
  • Symmetry: Icosahedral symmetry without reflection

Geometric Properties of the Snub Dodecahedron

The Snub Dodecahedron possesses the most sophisticated geometric properties:

Basic Parameters
  • Edge length (a): Length of all 150 edges
  • Faces: 92 regular polygons (80 triangles + 12 pentagons)
  • Euler characteristic: V - E + F = 60 - 150 + 92 = 2
  • Dual form: Pentagonal hexecontahedron
Special Properties
  • Chirality: No reflection symmetry - exists in mirror forms
  • Vertex figure: (3.3.3.3.5) - Four triangles and one pentagon
  • Icosahedral symmetry: 60 rotational symmetry operations
  • Snub operation: Result of "snubbing" a dodecahedron

Mathematical Relationships

The Snub Dodecahedron involves the most sophisticated mathematical relationships:

Golden Ratio φ
φ = (1+√5)/2 ≈ 1.618

The snub dodecahedron is fundamentally based on the golden ratio, like all pentagonal polyhedra.

Complex Parameter t
t ≈ 0.4716

A complex parameter involving nested cube roots that determines the snub dodecahedron's geometry.

Applications of the Snub Dodecahedron

Snub Dodecahedra find applications in the most advanced scientific fields:

Advanced Biology
  • Largest viral capsid structures and protein cages
  • Complex biomolecular assemblies and organelles
  • Advanced protein folding patterns
  • Sophisticated chiral biological structures
Cutting-Edge Materials
  • Ultimate chiral metamaterials and photonic crystals
  • Maximum complexity carbon cage structures
  • Advanced quasicrystalline materials
  • Sophisticated chiral liquid crystal phases
Theoretical Physics
  • Ultimate chiral symmetry and parity violation
  • Advanced topological phase transitions
  • Complex quantum state geometries
  • Sophisticated field theory applications
Advanced Engineering
  • Ultimate complexity architectural structures
  • Advanced aerospace and space applications
  • Sophisticated artistic and cultural installations
  • Maximum precision mechanical systems

Formulas for the Snub Dodecahedron

Golden Ratio φ
\[\phi = \frac{1+\sqrt{5}}{2} \approx 1.618\]

Fundamental constant for pentagonal geometry

Surface S
\[S = a^2(20\sqrt{3}+3\sqrt{25+10\sqrt{5}})\]

Surface area involving golden ratio and √3

Complex Parameter t
\[t = \frac{1}{12}(\sqrt[3]{44+12\phi(9+\sqrt{81\phi-15})} + \sqrt[3]{44+12\phi(9-\sqrt{81\phi-15})}-4)\]

Ultra-complex parameter ≈ 0.4716 defining snub geometry

Volume V
\[V = \frac{a^3}{6\sqrt{1-2t}}(3\sqrt{10(9t-2+(4t-1)\sqrt{5})}+20\sqrt{2+2t})\]

Most complex volume formula among all polyhedra

Outer radius rc
\[r_c = \frac{a}{2}\sqrt{\frac{2-2t}{1-2t}}\]

Circumradius involving complex parameter t

Midsphere radius rm
\[r_m = \frac{a}{2\sqrt{1-2t}}\]

Midsphere radius with parameter t

Edge length a (Inverse formulas)
\[a = \sqrt[3]{\frac{6\sqrt{1-2t} \cdot V}{3\sqrt{10(9t-2+(4t-1)\sqrt{5})}+20\sqrt{2+2t}}}\]

from volume

\[a = \sqrt{\frac{S}{20\sqrt{3}+3\sqrt{25+10\sqrt{5}}}}\]

from surface

\[a = \frac{2r_c}{\sqrt{\frac{2-2t}{1-2t}}}\]

from outer radius

\[a = r_m \cdot 2\sqrt{1-2t}\]

from midsphere radius

Calculate edge length from other parameters

Calculation Example for a Snub Dodecahedron

Given
Edge length a = 1

Find: All properties of the Snub Dodecahedron

1. Constants
\[\phi = \frac{1+\sqrt{5}}{2} \approx 1.618\] \[t \approx 0.4716\]

The fundamental constants for all calculations

2. Surface Calculation
\[S = 1^2(20\sqrt{3}+3\sqrt{25+10\sqrt{5}})\] \[S = 20 \times 1.732 + 3 \times 7.647\] \[S = 34.64 + 22.94\] \[S = 57.6\]

The surface area is approximately 57.6 square units

3. Volume Calculation
\[V = \frac{1^3}{6\sqrt{0.0568}}(3\sqrt{31.44}+20\sqrt{2.943})\] \[V = \frac{1}{1.431}(16.79 + 34.30)\] \[V = \frac{51.09}{1.431}\] \[V = 35.7\]

The volume is approximately 35.7 cubic units

4. Radii Calculations
\[r_c = \frac{1}{2}\sqrt{\frac{1.0568}{0.0568}} = 2.16\] \[r_m = \frac{1}{2\sqrt{0.0568}} = 2.10\]

Outer radius ≈ 2.16, Midsphere radius ≈ 2.10

5. Complete Snub Dodecahedron
Edge length a = 1.00 Volume V = 35.7
Surface S = 57.6 Outer radius rc = 2.16
Midsphere radius rm = 2.10 92 Total Faces

The most complex chiral Archimedean solid with all calculated properties

The Snub Dodecahedron: Ultimate Complexity in Chiral Geometry

The Snub Dodecahedron represents the absolute pinnacle of complexity among all Archimedean solids. As the largest chiral member of this exclusive family, it embodies the most sophisticated mathematical relationships while maintaining the elegant beauty that defines geometric perfection. With its 92 faces and intricate formulas involving both the golden ratio and complex algebraic parameters, it stands as the ultimate achievement in semi-regular polyhedral geometry.

Ultimate geometric complexity and pentagonal elegance

The Snub Dodecahedron achieves the maximum possible complexity within Archimedean constraints:

  • Maximum face count: 92 faces make it the largest Archimedean solid (80 triangles + 12 pentagons)
  • Chiral sophistication: Exists in left-handed and right-handed forms with no reflection symmetry
  • Pentagonal foundation: Built upon dodecahedral geometry with golden ratio proportions
  • Vertex configuration: Each vertex connects four triangles and one pentagon (3.3.3.3.5)
  • Icosahedral symmetry: 60 rotational symmetries creating the highest possible complexity
  • Snub operation mastery: The ultimate expression of "snubbing" applied to the dodecahedron

Golden ratio and ultra-complex parameter mathematics

Golden ratio foundation

The snub dodecahedron is fundamentally based on the golden ratio φ = (1+√5)/2, inheriting the pentagonal harmony that has fascinated mathematicians since ancient Greece. This connection links it to the deepest aesthetic principles in mathematics.

Parameter t complexity

The parameter t ≈ 0.4716 is defined by an extraordinarily complex expression involving nested cube roots of terms containing φ. This represents one of the most intricate constants in elementary geometry.

Computational extremes

The formulas push computational mathematics to its limits, requiring ultra-high precision arithmetic and sophisticated symbolic manipulation to achieve accurate results.

Mathematical uniqueness

No other polyhedron in classical geometry approaches the mathematical complexity of the snub dodecahedron, making it a singular achievement in geometric mathematics.

Construction and ultimate snub operation

The snub dodecahedron represents the pinnacle of snub construction techniques:

Ultimate snubbing

Starting with a dodecahedron, the snub operation simultaneously truncates all vertices while twisting the structure. This creates 80 new triangular faces while preserving the 12 pentagonal faces in modified form.

Chiral generation mastery

The twisting can occur in two mirror-image directions, creating the left-handed and right-handed forms. This chirality is irreducible and fundamental to the structure.

Dual complexity

Its dual, the pentagonal hexecontahedron, has 60 irregular pentagonal faces, each corresponding to a vertex of the snub dodecahedron. This dual is equally chiral and complex.

Vertex uniformity achievement

Despite the overwhelming complexity, all 60 vertices remain geometrically identical, maintaining the fundamental Archimedean requirement through mathematical precision.

Advanced scientific and technological applications

The ultimate complexity of the snub dodecahedron makes it valuable in the most advanced applications:

  • Virology extremes: Models for the largest and most complex viral capsids known to science
  • Supramolecular chemistry: Templates for the most sophisticated molecular cages and containers ever designed
  • Advanced nanotechnology: Blueprints for nanostructures requiring maximum surface complexity and chiral properties
  • Quasicrystalline materials: Understanding the most complex aperiodic structures and their unique properties
  • Photonic crystals: Design of chiral optical devices with unprecedented complexity and functionality
  • Theoretical physics: Models for the most subtle chiral effects and symmetry breaking phenomena
  • Computational mathematics: Ultimate benchmark problems for testing symbolic computation and high-precision algorithms

Mathematical formulas and computational frontiers

Formula sophistication

The volume formula alone involves nested square roots, complex parameters, and multiple radical expressions. It represents the most intricate volume calculation in classical geometry.

Surface area elegance

Despite the complex volume formula, the surface area expression maintains relative elegance while still incorporating both √3 and golden ratio terms, showing the deep mathematical structure.

Computational challenges

The nested radical expressions and complex parameter definitions require the most sophisticated computational techniques available, pushing the boundaries of numerical analysis.

Symbolic computation limits

Computer algebra systems reach their limits when handling the exact symbolic expressions, making the snub dodecahedron a true test of mathematical software capabilities.

Philosophical and aesthetic pinnacle

Ultimate complexity

The snub dodecahedron represents the absolute limit of complexity achievable within the constraints of vertex uniformity, demonstrating that mathematical beauty and extreme sophistication can coexist.

Chiral mastery

As the most complex chiral object in classical geometry, it embodies the concept of handedness in its most sophisticated form, connecting to the deepest principles of symmetry and asymmetry.

Mathematical completeness

Its existence proves the richness and completeness of the Archimedean classification, showing that even within strict geometric constraints, unlimited complexity is possible.

Aesthetic transcendence

The snub dodecahedron transcends mere calculation to become a work of mathematical art, proving that the most complex structures can also be the most beautiful.

Summary

The Snub Dodecahedron stands as the ultimate achievement in chiral polyhedral geometry, representing the perfect synthesis of maximum complexity and mathematical elegance. With its 92 faces, intricate formulas involving both the golden ratio and ultra-complex algebraic parameters, it pushes the boundaries of geometric possibility while maintaining the strict vertex uniformity that defines Archimedean solids. From the largest viral structures to the most sophisticated metamaterials, from advanced theoretical physics to cutting-edge computational mathematics, the snub dodecahedron continues to inspire and challenge researchers across all scientific disciplines. Its existence proves that there are no limits to the complexity and beauty that can emerge from mathematical principles, serving as an eternal reminder that the universe's most sophisticated structures often reveal the deepest truths about the nature of space, symmetry, and mathematical reality itself.

Cuboctahedron • Icosidodecahedron • Rhombicosidodecahedron • Rhombicuboctahedron • Snub cube • Truncated cube • Snub dodecahedron • Truncated cuboctahedron • Truncated dodecahedron • Truncated icosahedron • Truncated icosidodecahedron • Truncated octahedron • Truncated tetrahedron