Matrix X-Axis Rotation
Calculator for the rotation of a 3x3 matrix around the X axis
X-Axis Rotation Calculator
Instructions
Enter the rotation angle for rotation around the X-axis.
- Unit: Switch between degrees or radians
- Mode: Active (rotate object) or Passive (rotate coordinates)
X-Axis Rotation - Overview
X-Axis Rotation
The X-axis rotation (Roll) rotates objects or coordinates around the X-axis. The matrix rotation distinguishes between active and passive rotation.
Rotation Matrix Formula
The general formula for rotation around the X-axis:
\(R_x(\alpha) = \begin{bmatrix} 1 & 0 & 0\\ 0 & \cos \alpha & -\sin \alpha\\ 0 & \sin \alpha & \cos \alpha \end{bmatrix}\)
Example: 90° Rotation
Active rotation (counterclockwise):
\(R_x(90°) = \begin{bmatrix} 1 & 0 & 0\\ 0 & 0 & -1\\ 0 & 1 & 0 \end{bmatrix}\)
Rotation Modes
- Active Rotation: Rotates the vector/object in the coordinate system (counterclockwise). Also called geometric transformation.
- Passive Rotation: Rotates the coordinate system (clockwise). The vector remains unchanged.
|
|
Description of Matrix X-Axis Rotation
Active Rotation
With active rotation, the vector or the object is rotated in the coordinate system. The active rotation is also called a geometric transformation. The rotation is counterclockwise.
Example: 90° Rotation of the X-axis
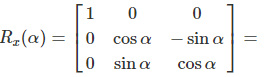

Properties
- Axis: Rotation around X-axis (Roll)
- Direction: Counterclockwise (when looking along positive X-axis)
- First row: Always [1, 0, 0] (X-component unchanged)
- Orthogonal: RT = R-1
- Determinant: det(R) = 1
Passive Rotation
With passive rotation, the coordinate system is rotated. The vector remains unchanged. The rotation is clockwise.
Example: 90° Rotation of the X-axis
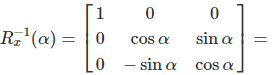
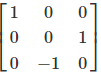
Matrix Structure
Active Rotation (counterclockwise):
\(R_x(\alpha) = \begin{bmatrix} 1 & 0 & 0\\ 0 & \cos \alpha & -\sin \alpha\\ 0 & \sin \alpha & \cos \alpha \end{bmatrix}\)
Passive Rotation (clockwise):
\(R_x^{-1}(\alpha) = \begin{bmatrix} 1 & 0 & 0\\ 0 & \cos \alpha & \sin \alpha\\ 0 & -\sin \alpha & \cos \alpha \end{bmatrix}\)
Practical Applications
Aerospace & Robotics:
- Aircraft roll control
- Drone stabilization
- Robotic arm wrist rotation
- Satellite roll axis control
Computer Graphics & Gaming:
- Camera roll effects
- Object barrel roll animations
- Character rotation around longitudinal axis
- Flight simulators
Key Characteristics
The X-axis rotation matrix is unique in that its first row remains constant [1, 0, 0], meaning the X-component of any vector is unchanged during rotation. Only the Y and Z components are affected. This rotation is commonly called "Roll" in aerospace applications and represents rotation around the longitudinal axis of an object.
Related Rotations
For complete 3D orientation, you may need to combine rotations around multiple axes:
- Y-axis rotation (Pitch): Nose up/down rotation
- Z-axis rotation (Yaw): Left/right rotation
- Combined rotations: Use Euler angles or quaternions for full 3D rotation
|
|