Matrix YawPitchRoll Rotation (Quaternion)
Online calculator for calculating the rotation around the X, Y and Z axes of a 3x3 matrix
XYZ Axis Rotation Calculator
Instructions
This function calculates the 3D rotation of a solid using the quaternion (avoids gimbal lock problem).
- Unit: Switch between degrees or radians
- Mode: Active (rotate object) or Passive (rotate coordinates)
- Order: Roll-Pitch-Yaw (Z → X → Y)
Quaternion Rotation - Overview
Quaternion Advantage
The quaternion is an extension of complex numbers. In contrast to rotation with Euler angles, this avoids the gimbal lock problem that arises when two axes of rotation are superimposed.
Rotation Order
The calculator assumes a Roll-Pitch-Yaw rotation order:
- First: Rotation around Z-axis (Yaw)
- Second: Rotation around X-axis (Roll)
- Third: Rotation around Y-axis (Pitch)
Important Note
The matrices of the two methods (quaternion vs. Euler angles) differ because the assignment of the axes and the order of calculation is different. See the Euler angles calculator for comparison.
Rotation Modes
- Active Rotation: Rotates the vector/object in the coordinate system (counterclockwise). Also called geometric transformation.
- Passive Rotation: Rotates the coordinate system (clockwise). The vector remains unchanged.
|
|
Matrix Rotation with Quaternion
Active Rotation
With active rotation, the vector or the object is rotated in the coordinate system. The active rotation is also called a geometric transformation. The rotation is counterclockwise.
Example: 90° Rotation
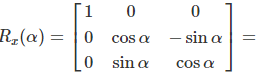

Quaternion Benefits
- No gimbal lock: Avoids axis alignment problems
- Smooth interpolation: Better for animations
- Efficient: Fewer operations for combined rotations
- Compact: Uses 4 values instead of 9 (matrix)
- Stable: Better numerical stability
Passive Rotation
With passive rotation, the coordinate system is rotated. The vector remains unchanged. The rotation is clockwise.
Example: 90° Rotation
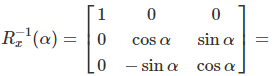

Differences from Euler Angles
- Axis assignment: Different order of rotations
- Calculation order: Z → X → Y (not Z → Y → X)
- Result matrix: Different values for same angles
- No gimbal lock: Works at all angle combinations
Yaw, Pitch, Roll Rotation
A 3D body can be rotated around three axes. These rotations are called yaw, pitch, and roll.
Yaw (Z-axis)
Yaw is the counterclockwise rotation of the Z-axis:
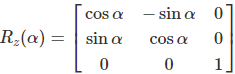
Pitch (Y-axis)
Pitch is the counterclockwise rotation of the Y-axis:
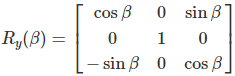
Roll (X-axis)
Roll is the counterclockwise rotation of the X-axis:
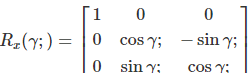
Formulas of Yaw, Pitch, Roll Rotation
Each rotation matrix is a simple extension of the 2D rotation matrix. For example, the Yaw matrix essentially performs a 2D rotation with respect to the Z-coordinate while the Z-coordinate remains unchanged. So the third row and the third column look like part of the identity matrix, while the top left part looks like the 2D rotation matrix.
The yaw, pitch and roll rotations can be used to place a 3D body in any direction. A single rotation matrix can be formed by multiplying the matrices.
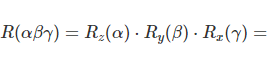
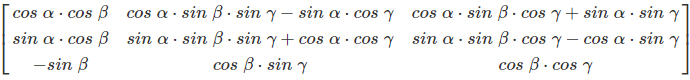
Practical Applications
Aerospace & Robotics:
- Spacecraft attitude control
- Drone flight controllers
- Robotic manipulator control
- Inertial navigation systems
Computer Graphics & Gaming:
- Smooth camera rotations
- Character animation blending
- VR/AR orientation tracking
- 3D object interpolation
Why Use Quaternions?
Quaternions are preferred over Euler angles in applications requiring smooth continuous rotation (animations, flight control) or where gimbal lock must be avoided (when pitch approaches ±90°). They provide better interpolation and are more computationally efficient for combining multiple rotations. For more information about Euler angles rotation, see here.
|
|