Matrix Scalar Multiplication 3×3
Online calculator for multiplying a 3x3 matrix by a real number
Matrix-Scalar Multiplication Calculator
Instructions
Enter the values of the matrix and the scalar (real number). Empty fields are counted as zero. Click Calculate.
Scalar Multiplication - Overview
What is Scalar Multiplication?
Matrices can be multiplied with real numbers. The real number is called a scalar to distinguish it from matrices. Each element of the matrix is multiplied by the scalar.
Calculation Formula
Matrices and scalar are multiplied by multiplying the individual elements of the matrix with the scalar:
\(k \cdot A = k \cdot \begin{bmatrix}a_{11} & a_{12} & a_{13}\\a_{21} & a_{22} & a_{23}\\a_{31} & a_{32} & a_{33}\end{bmatrix} = \begin{bmatrix}k \cdot a_{11} & k \cdot a_{12} & k \cdot a_{13}\\k \cdot a_{21} & k \cdot a_{22} & k \cdot a_{23}\\k \cdot a_{31} & k \cdot a_{32} & k \cdot a_{33}\end{bmatrix}\)
Example
Given:
\(\displaystyle A = \begin{bmatrix}1 & 2 & 3\\4 & 5 & 6\\7 & 8 & 9\end{bmatrix}, \quad k = 3\)
Calculation:
\(3 \cdot A = \begin{bmatrix}3 \cdot 1 & 3 \cdot 2 & 3 \cdot 3\\3 \cdot 4 & 3 \cdot 5 & 3 \cdot 6\\3 \cdot 7 & 3 \cdot 8 & 3 \cdot 9\end{bmatrix}\)
Result:
\(= \begin{bmatrix}3 & 6 & 9\\12 & 15 & 18\\21 & 24 & 27\end{bmatrix}\)
Properties
- Commutative: k · A = A · k
- Associative: (k · m) · A = k · (m · A)
- Distributive (scalars): (k + m) · A = k · A + m · A
- Distributive (matrices): k · (A + B) = k · A + k · B
- Identity: 1 · A = A
- Zero: 0 · A = 0 (zero matrix)
|
|
Description of Matrix-Scalar Multiplication
Fundamentals
Matrices can be multiplied with real numbers. The real number is called a scalar to distinguish it from matrices. This is one of the simplest operations in matrix algebra.
General Formula:
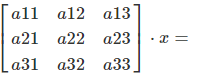
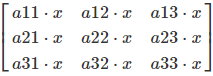
How It Works
Matrices and scalar are multiplied by multiplying the individual elements of the matrix with the scalar. Every single element in the matrix is multiplied by the same scalar value.
- Take the scalar value (e.g., k = 3)
- Multiply each element of the matrix by k
- The result is a new matrix with the same dimensions
Detailed Example
Step-by-Step Calculation
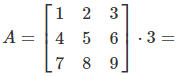
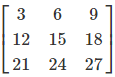
Important Properties
- Commutative: k · A = A · k (order doesn't matter)
- Associative: (k · m) · A = k · (m · A)
- Distributive over addition: k · (A + B) = k · A + k · B
- Distributive over scalars: (k + m) · A = k · A + m · A
- Identity element: 1 · A = A
- Zero element: 0 · A = 0 (zero matrix)
- Negative: (-1) · A = -A
Practical Applications
Mathematics & Physics:
- Scaling vectors and transformations
- Adjusting physical quantities proportionally
- Solving differential equations
- Eigenvalue and eigenvector calculations
Engineering & Computer Science:
- 3D graphics scaling transformations
- Image processing (brightness adjustment)
- Machine learning (weight updates)
- Signal processing (amplification/attenuation)
Why Scalar Multiplication is Important
Scalar multiplication is one of the fundamental operations in linear algebra. It's used extensively in combination with other matrix operations to solve systems of equations, perform transformations, and in many algorithms in computer science and engineering. Unlike matrix multiplication, scalar multiplication is commutative and much simpler to compute.
|
|