Yaw-Pitch-Roll Rotation (XYZ) 4×4
Calculator for combined rotation around X, Y, and Z axes
XYZ Rotation Calculator
Instructions
Enter the rotation angles for X (Pitch), Y (Yaw), and Z (Roll) axes. Choose between active or passive rotation mode.
Yaw-Pitch-Roll - Overview
What is Yaw-Pitch-Roll?
Yaw-Pitch-Roll (also called Euler angles) describes a 3D body's orientation using three sequential rotations around the Z, Y, and X axes respectively.
Combined Rotation Formula
The combined rotation matrix is the product:
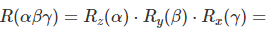
The Three Rotations
- Roll (Z-axis): Bank angle - tilt left/right
- Pitch (Y-axis): Elevation - nose up/down
- Yaw (X-axis): Heading - turn left/right
Important
- Order matters: Rz·Ry·Rx ≠ Rx·Ry·Rz
- Gimbal lock: Can occur at ±90° pitch
- Convention: Z-Y-X order (intrinsic rotations)
|
|
Description of Yaw-Pitch-Roll Rotation
Fundamentals
A 3D body can be rotated around three axes. These rotations are called Yaw, Pitch, Roll (or Euler angles). The matrix rotation distinguishes between active and passive rotation.
Active Rotation
With active rotation, the vector or the object is rotated in the coordinate system. The active rotation is also called a geometric transformation. The rotation is counterclockwise.
Example rotation formulas:
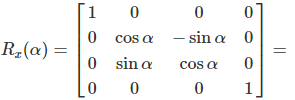

Passive Rotation
With passive rotation, the coordinate system is rotated. The vector remains unchanged. The rotation is clockwise.
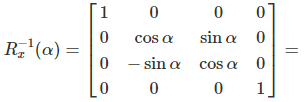

The Three Rotations
Roll (Z-Axis)
Roll is the counterclockwise rotation of the Z-axis. The rotation matrix looks like this:
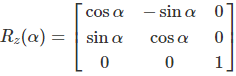
Pitch (Y-Axis)
Pitch is the counterclockwise rotation of the Y-axis. The rotation matrix for this is:
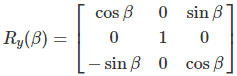
Yaw (X-Axis)
Yaw is the counterclockwise rotation of the X-axis. The rotation matrix for the X-axis is:
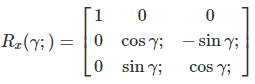
Combined Rotation Formula
Each rotation matrix is a simple extension of the 2D rotation matrix. For example, the Roll matrix essentially performs a 2D rotation with respect to the X and Y coordinates while the Z coordinate remains unchanged. So the third row and the third column look like part of the identity matrix, while the top left part looks like the 2D rotation matrix.
The yaw, pitch and roll rotations can be used to place a 3D body in any direction. A single rotation matrix can be formed by multiplying the matrices:
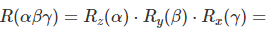
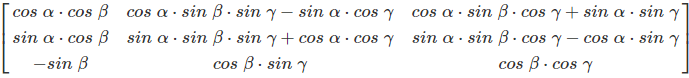
Practical Applications
Aviation & Aerospace:
- Aircraft orientation: Complete attitude description
- Flight simulation: Realistic aircraft control
- Autopilot systems: Attitude control
- Spacecraft pointing: Antenna and sensor orientation
Gaming & Robotics:
- Camera control: First/third person view orientation
- Character animation: Head and body orientation
- Robot arm control: End-effector orientation
- VR/AR headsets: User head tracking
Rotation Order Matters!
Different Rotation Orders:
- Z-Y-X (Yaw-Pitch-Roll): Common in aviation
- X-Y-Z: Used in some robotics
- Z-X-Z: Classical Euler angles
- Each gives different results!
Example:
Rotating 90° around X then 90° around Y gives a different result than rotating 90° around Y then 90° around X. This is because matrix multiplication is not commutative:
Rz·Ry·Rx ≠ Rx·Ry·Rz
Gimbal Lock Problem
Gimbal lock is a serious issue with Euler angles that occurs when the pitch angle reaches ±90°. At this configuration:
What happens:
- Two axes become aligned
- Loss of one degree of freedom
- Cannot represent certain orientations
- Rotations become unpredictable
Solutions:
- Quaternions: No gimbal lock (recommended!)
- Axis-angle: Alternative representation
- Different rotation order: May help in some cases
- Avoid ±90° pitch: Software constraints
Mathematical Properties
Combined Rotation Properties:
- Orthogonal: RTR = I
- Determinant: det(R) = 1
- Inverse: R-1 = RT
- Preserves lengths and angles
Conversion:
- To Quaternion: More stable
- To Axis-Angle: Single rotation
- To Rotation Matrix: This calculator
- Back to Euler: Multiple solutions possible
Aviation Terminology
Roll (Bank):
- Rotation around longitudinal axis
- Wings tilt left or right
- Controls: Ailerons
- Range: typically ±180°
Pitch (Elevation):
- Rotation around lateral axis
- Nose points up or down
- Controls: Elevators
- Range: typically ±90°
Yaw (Heading):
- Rotation around vertical axis
- Nose turns left or right
- Controls: Rudder
- Range: 0° to 360° (compass)
Understanding the Calculation
This calculator computes the combined rotation matrix by multiplying three individual rotation matrices in the order: Rz(roll) · Ry(pitch) · Rx(yaw). This is the standard Z-Y-X Euler angle convention used in aviation. The resulting 4×4 matrix can be used to transform 3D points or vectors by the specified orientation. For gimbal-lock-free rotations, consider using quaternions instead, especially for smooth animation interpolation or when rotations exceed ±90° pitch.
|
|