Matrix Scalar Multiplication 4×4
Calculator for multiplying a 4x4 matrix by a real number (scalar)
Scalar Multiplication Calculator
Instructions
Enter the matrix values and the scalar (real number) to multiply with. Empty fields are counted as zero. Click Calculate.
Scalar Multiplication - Overview
What is Scalar Multiplication?
Scalar multiplication multiplies every element of a matrix by a real number (scalar). The scalar is a single number that scales the entire matrix uniformly.
Calculation Formula
Each element of the matrix is multiplied by the scalar:
\(k \cdot A = [k \cdot a_{ij}]\) for all elements \(a_{ij}\)
Example (2×2)
\(3 \cdot \begin{bmatrix}1 & 2\\3 & 4\end{bmatrix} = \begin{bmatrix}3 & 6\\9 & 12\end{bmatrix}\)
Properties
- Commutative: k·A = A·k
- Associative: (k·m)·A = k·(m·A)
- Distributive over matrix addition: k·(A+B) = k·A + k·B
- Distributive over scalar addition: (k+m)·A = k·A + m·A
- Identity: 1·A = A
- Zero: 0·A = 0 (zero matrix)
|
|
Description of Matrix Scalar Multiplication
Fundamentals
Matrices can be multiplied with real numbers. The real number is called a scalar to distinguish it from matrices. This is one of the simplest and most fundamental operations in linear algebra.
General Formula (4×4):
Matrices and scalar are multiplied by multiplying each individual element of the matrix with the scalar:
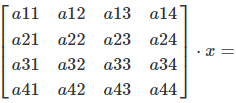

How It Works
- Take the scalar (real number k)
- Multiply k with the first element a₁₁
- Multiply k with the second element a₁₂
- Repeat for all 16 elements
- Result: New matrix with all elements scaled by k
Visual Example
Complete Example (4×4)
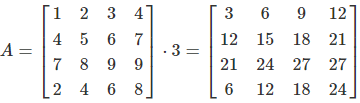
Step-by-Step Calculation:
For each element, multiply by the scalar:
- Element (1,1): 1 × 3 = 3
- Element (1,2): 2 × 3 = 6
- Element (1,3): 3 × 3 = 9
- Element (1,4): 4 × 3 = 12
- ...and so on for all 16 elements
Special Scalars
- k = 1: Identity (A remains unchanged)
- k = 0: Zero matrix (all elements become 0)
- k = -1: Negation (all signs flip)
- k = 2: Doubling (all elements doubled)
- k = 0.5: Halving (all elements halved)
Practical Applications
3D Graphics & Gaming:
- Uniform scaling: Scale objects in all directions equally
- Brightness adjustment: Color matrices scaled for lighting
- Animation speed: Time-based transformations scaled
- Normalization: Scale to unit size
Mathematics & Physics:
- Unit conversion: Scale measurements (meters to feet)
- Normalization: Scale vectors/matrices to standard form
- Amplification: Increase/decrease signal strength
- System scaling: Scale entire equation systems
Mathematical Properties
Basic Properties:
- Commutativity: k·A = A·k (order doesn't matter)
- Associativity: (k·m)·A = k·(m·A) = (k·m)·A
- Identity element: 1·A = A
- Zero element: 0·A = 0 (zero matrix)
Distributive Properties:
- Over matrix addition: k·(A + B) = k·A + k·B
- Over scalar addition: (k + m)·A = k·A + m·A
- With matrix multiplication: k·(A·B) = (k·A)·B = A·(k·B)
- With determinant: det(k·A) = k⁴·det(A) for 4×4
Computational Efficiency
For 4×4 Matrices:
- 16 multiplications (one per element)
- 0 additions (no summation needed)
- Complexity: O(n²) for n×n matrices
- Very fast operation compared to matrix multiplication
Optimization:
- SIMD: All elements can be multiplied in parallel
- GPU-friendly: Highly parallelizable operation
- Cache-efficient: Sequential memory access
- In-place: Can overwrite original matrix
Important Notes
- Uniform scaling only: Scalar multiplication scales all dimensions equally. For non-uniform scaling (different factors for x, y, z), use a diagonal scaling matrix instead.
- Preserves structure: Scalar multiplication preserves the "shape" of the matrix data, only changing the magnitude.
- Effect on determinant: For a 4×4 matrix, multiplying by scalar k changes the determinant by k⁴ (to the power of matrix dimension).
- Commutative with ALL operations: Unlike matrix multiplication, scalar multiplication commutes with everything.
Geometric Interpretation
In 3D graphics, multiplying a transformation matrix by a scalar:
k > 1:
- Scales the transformation up
- Objects become larger
- Translations become longer
0 < k < 1:
- Scales the transformation down
- Objects become smaller
- Translations become shorter
k = -1: Creates a reflection through the origin (inverts all transformations).
|
|