Matrix Addition 4×4
Online calculator for adding two 4x4 matrices
Matrix Addition Calculator
Instructions
Enter the values of both matrices to be added. Empty fields are counted as zero. Click Calculate.
Matrix Addition - Overview
Prerequisites
To add matrices, the matrices must match. That is, they must have the same number of rows and columns. Both matrices must be 4×4.
Calculation Formula
In order to perform a matrix addition, the corresponding matrix elements are added:
\(C_{ij} = A_{ij} + B_{ij}\)
Example (3x3)
\(\begin{bmatrix}1 & 2 & 3\\4 & 5 & 6\\7 & 8 & 9\end{bmatrix} + \begin{bmatrix}1 & 4 & 7\\2 & 5 & 8\\3 & 6 & 9\end{bmatrix} = \begin{bmatrix}2 & 6 & 10\\6 & 10 & 14\\10 & 14 & 18\end{bmatrix}\)
Properties
- Commutative: A + B = B + A
- Associative: (A + B) + C = A + (B + C)
- Identity: A + 0 = A (zero matrix)
- Inverse: A + (−A) = 0
- Same dimensions: Result has same size as inputs
|
|
Description of Matrix Addition
Fundamentals
To add matrices, the matrices must match. That is, they must have the same number of rows and the same number of columns. This is one of the basic operations in matrix algebra.
General Formula (4×4):
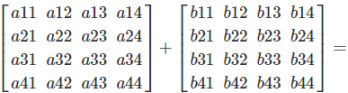
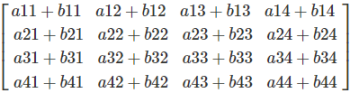
How It Works
In order to perform a matrix addition, the corresponding matrix elements are added. Each element in position (i,j) of matrix A is added to the corresponding element at position (i,j) in matrix B.
- Check dimensions: Both matrices must be 4×4
- Add each element: Cij = Aij + Bij
- The result is a new matrix with the same dimensions
Detailed Example (3×3)
Step-by-Step Calculation
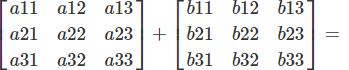
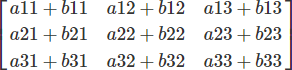
Complete Example:
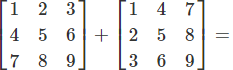
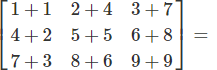

Practical Applications
Mathematics & Physics:
- Combining transformations in 3D graphics (4×4 homogeneous matrices)
- Adding force or velocity vectors in physics
- Solving systems of linear equations
- Quantum mechanics state calculations
Engineering & Computer Science:
- 3D computer graphics (combining transformations)
- Neural networks (layer combinations)
- Robotics (pose additions)
- Game development (object positioning)
Why 4×4 Matrices?
4×4 matrices are particularly important in 3D computer graphics and robotics. They use homogeneous coordinates to represent translations, rotations, and scaling in a single matrix. The fourth row/column allows for perspective projection and makes it possible to combine all transformations through matrix multiplication.
|
|