Matrix Y-Axis Rotation
Calculator for the rotation of a 3x3 matrix around the Y axis
Y-Axis Rotation Calculator
Instructions
Enter the rotation angle for rotation around the Y-axis.
- Unit: Switch between degrees or radians
- Mode: Active (rotate object) or Passive (rotate coordinates)
Y-Axis Rotation - Overview
Y-Axis Rotation
The Y-axis rotation (Pitch) rotates objects or coordinates around the Y-axis. The matrix rotation distinguishes between active and passive rotation.
Rotation Matrix Formula
The general formula for rotation around the Y-axis:
\(R_y(\alpha) = \begin{bmatrix} \cos \alpha & 0 & \sin \alpha\\ 0 & 1 & 0\\ -\sin \alpha & 0 & \cos \alpha \end{bmatrix}\)
Example: 90° Rotation
Active rotation (counterclockwise):
\(R_y(90°) = \begin{bmatrix} 0 & 0 & 1\\ 0 & 1 & 0\\ -1 & 0 & 0 \end{bmatrix}\)
Rotation Modes
- Active Rotation: Rotates the vector/object in the coordinate system (counterclockwise). Also called geometric transformation.
- Passive Rotation: Rotates the coordinate system (clockwise). The vector remains unchanged.
|
|
Description of Matrix Y-Axis Rotation
Active Rotation
With active rotation, the vector or the object is rotated in the coordinate system. The active rotation is also called a geometric transformation. The rotation is counterclockwise.
Example: 90° Rotation of the Y-axis
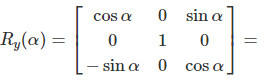

Properties
- Axis: Rotation around Y-axis (Pitch)
- Direction: Counterclockwise (when looking along positive Y-axis)
- Second row: Always [0, 1, 0] (Y-component unchanged)
- Orthogonal: RT = R-1
- Determinant: det(R) = 1
Passive Rotation
With passive rotation, the coordinate system is rotated. The vector remains unchanged. The rotation is clockwise.
Example: 90° Rotation of the Y-axis
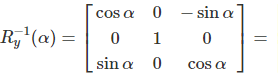

Matrix Structure
Active Rotation (counterclockwise):
\(R_y(\alpha) = \begin{bmatrix} \cos \alpha & 0 & \sin \alpha\\ 0 & 1 & 0\\ -\sin \alpha & 0 & \cos \alpha \end{bmatrix}\)
Passive Rotation (clockwise):
\(R_y^{-1}(\alpha) = \begin{bmatrix} \cos \alpha & 0 & -\sin \alpha\\ 0 & 1 & 0\\ \sin \alpha & 0 & \cos \alpha \end{bmatrix}\)
Practical Applications
Aerospace & Robotics:
- Aircraft pitch control (nose up/down)
- Drone elevation control
- Robotic arm elbow rotation
- Satellite pitch axis control
Computer Graphics & Gaming:
- Camera pitch (looking up/down)
- Object tilt animations
- Character nod animations
- Flight simulators pitch control
Key Characteristics
The Y-axis rotation matrix is unique in that its second row remains constant [0, 1, 0], meaning the Y-component of any vector is unchanged during rotation. Only the X and Z components are affected. This rotation is commonly called "Pitch" in aerospace applications and represents nose-up or nose-down rotation. Note the asymmetry in the formula compared to X and Z rotations.
Related Rotations
For complete 3D orientation, you may need to combine rotations around multiple axes:
- X-axis rotation (Roll): Barrel roll rotation
- Z-axis rotation (Yaw): Left/right rotation
- Combined rotations: Use Euler angles or quaternions for full 3D rotation
|
|