Matrix Multiplication 4×4
Calculator for multiplying 4x4 matrices
Matrix Multiplication Calculator
Instructions
Enter the values of both matrices to be multiplied. Empty fields are counted as zero. Click Calculate.
Matrix Multiplication - Overview
Prerequisites
Two matrices can be multiplied if the number of columns in the left matrix is the same as the number of rows in the right matrix. For 4×4 matrices, this is always satisfied.
Calculation Formula
The product of a matrix is calculated by calculating the product sums of the pairs from the row vectors of the first matrix and the column vectors of the second matrix:
\(C_{ij} = \sum_{k=1}^{4} A_{ik} \cdot B_{kj}\)
Example
Calculating element C11:
\(C_{11} = A_{11} \cdot B_{11} + A_{12} \cdot B_{21} + A_{13} \cdot B_{31} + A_{14} \cdot B_{41}\)
Properties
- Not commutative: A × B ≠ B × A (order matters!)
- Associative: (A × B) × C = A × (B × C)
- Distributive: A × (B + C) = A × B + A × C
- Identity: A × I = I × A = A
- Dimension: (4×4) × (4×4) = (4×4)
Description of Matrix Multiplication
Fundamentals
There is a special rule for multiplication of matrices constructed in such a way that they can represent simultaneous equations using matrices.
Key Rules:
- Two matrices can be multiplied if the number of columns in the left matrix is the same as the number of rows in the right matrix.
- The product of a matrix is calculated by calculating the product sums of the pairs from the row vectors of the first matrix and the column vectors of the second matrix.
- For 4×4 matrices, each element requires 4 multiplications and 3 additions.
Calculation Steps
- Select a row from matrix A (i-th row)
- Select a column from matrix B (j-th column)
- Multiply corresponding elements (4 multiplications)
- Sum all the products (3 additions)
- Place result at position Cij
- Repeat for all 16 positions
Visual Examples
Matrix Multiplication Visualization
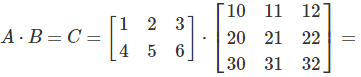
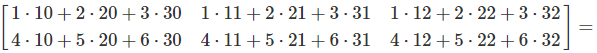
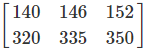
First Element Calculation:
The first element of the product \(C\), is the sum of the products of each element of the first row of \(A\), and the corresponding element of the first column of \(B\):
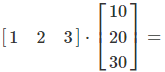
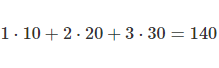
Practical Applications of 4×4 Matrix Multiplication
3D Graphics & Gaming:
- Transformation chains: Combining rotation, scaling, translation
- Camera view matrices: World-to-screen transformation
- Model hierarchies: Parent-child transformations
- Skeletal animation: Bone transformation chains
Robotics & Engineering:
- Forward kinematics: Joint-to-end-effector position
- Coordinate transformations: Between reference frames
- Pose composition: Combining multiple movements
- Homogeneous coordinates: Unified translation/rotation
Important Note
Matrix multiplication is NOT commutative! This means A × B ≠ B × A. The order of multiplication is crucial, especially in 3D graphics where the order of transformations matters. For example, "rotate then translate" produces a different result than "translate then rotate". A 4×4 matrix multiplication requires 64 multiplications and 48 additions (4 operations per element, 16 elements total).
Computational Complexity
For 4×4 Matrices:
- 16 elements to compute
- 4 multiplications per element
- 3 additions per element
- Total: 64 multiplications, 48 additions
- Complexity: O(n³) for n×n matrices
Optimization Techniques:
- SIMD instructions: Parallel computation
- GPU acceleration: Highly parallelizable
- Cache optimization: Memory access patterns
- Strassen algorithm: O(n^2.807) for large matrices
Why 4×4 Matrices in Computer Graphics?
4×4 matrices use homogeneous coordinates to represent 3D transformations. The extra dimension allows:
- Translation: Can be represented as matrix multiplication (not possible with 3×3)
- Perspective projection: Depth division for realistic perspective
- Unified operations: All transformations (rotation, scale, translation) in one matrix
- Transformation chains: Multiple operations combined through multiplication
- Standard in APIs: OpenGL, DirectX, Vulkan all use 4×4 matrices
|
|