Abgeschrägtes Dodekaeder berechnen
Rechner und Formeln zur Berechnung des abgeschrägten Dodekaeders
Abgeschrägtes Dodekaeder Rechner
Das abgeschrägte Dodekaeder
Ein abgeschrägtes Dodekaeder ist ein archimedischer Körper mit 92 Flächen: 12 regelmäßige Fünfecke und 80 gleichseitige Dreiecke.
Dodekaeder-Struktur
Ein abgeschrägtes Dodekaeder ist ein archimedischer Körper.
Es kombiniert regelmäßige Fünfecke und gleichseitige Dreiecke.
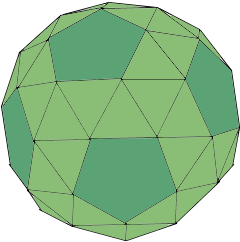
● 12 Fünfecke ● 80 Dreiecke ● 60 Ecken
|
|
Was ist ein abgeschrägtes Dodekaeder?
Ein abgeschrägtes Dodekaeder ist einer der 13 archimedischen Körper:
- 92 Flächen: 12 regelmäßige Fünfecke und 80 gleichseitige Dreiecke
- 60 Ecken: Jede Ecke wird von 4 Dreiecken und 1 Fünfeck gebildet
- 150 Kanten: Alle Kanten haben die gleiche Länge
- Chiralität: Existiert in zwei spiegelbildlichen Formen
- Symmetrie: Ikosaedrische Symmetriegruppe
- Goldener Schnitt: Maße stehen im Verhältnis des goldenen Schnitts
Geometrische Eigenschaften
Das abgeschrägte Dodekaeder besitzt faszinierende geometrische Eigenschaften:
Flächenstruktur
- 12 Fünfecke: Regelmäßige Pentagon-Flächen
- 80 Dreiecke: Gleichseitige dreieckige Flächen
- Einheitliche Kanten: Alle 150 Kanten sind gleich lang
- Vertex-Figur: Jede Ecke: 4 Dreiecke + 1 Fünfeck
Besondere Eigenschaften
- Chiralität: Rechts- und linkshändige Formen
- Ikosaedrische Symmetrie: 60 Symmetrieoperationen
- Goldener Schnitt: φ = (1+√5)/2 ≈ 1.618
- Konvexer Körper: Alle Innenwinkel < 180°
Mathematische Beziehungen
Das abgeschrägte Dodekaeder folgt komplexen mathematischen Gesetzen:
Volumenberechnung
Das Volumen hängt vom goldenen Schnitt φ und dem trigonometrischen Parameter t ab.
Oberflächenberechnung
Die Oberfläche kombiniert die Flächen von Dreiecken und Fünfecken.
Anwendungen des abgeschrägten Dodekaeders
Abgeschrägte Dodekaeder finden sich in verschiedenen Bereichen:
Wissenschaft & Forschung
- Kristallographie und Molekularstrukturen
- Fullerene und Carbon-Nanostrukturen
- Viruskapside und biologische Strukturen
- Mathematische Modellierung komplexer Systeme
Kunst & Design
- Architektonische Kuppel- und Dachstrukturen
- Skulpturen und geometrische Kunstwerke
- Schmuckdesign und Ornamentik
- 3D-Druck und moderne Fertigungstechnik
Spiele & Unterhaltung
- Würfelspiele und Gaming-Accessories
- Puzzle und mathematische Spielzeuge
- Geodätische Konstruktionen
- Virtual Reality und 3D-Modellierung
Technik & Engineering
- Optische Komponenten und Linsen
- Antennendesign und Empfangsstrukturen
- Stabilisierende Strukturelemente
- Biomimetische Konstruktionen
Formeln für das abgeschrägte Dodekaeder
Goldener Schnitt φ
Fundamentale Konstante für alle Berechnungen
Parameter t
Kosinus des kleineren Zentriwinkels ζ
Volumen V
Komplexe Formel mit goldenen Schnitt-Beziehungen
Oberfläche S
Summe der Flächen von Dreiecken und Fünfecken
Umkugelradius rc
Radius der umschreibenden Kugel
Kantenradius rm
Radius der Kugel durch Kantenmittelpunkte
Rechenbeispiel für ein abgeschrägtes Dodekaeder
Gegeben
Gesucht: Alle Eigenschaften des abgeschrägten Dodekaeders
1. Konstanten berechnen
Goldener Schnitt und trigonometrischer Parameter
2. Oberflächenberechnung
Oberfläche aus Seitenlänge
3. Volumenberechnung
Komplexe Volumenformel anwenden
4. Radien berechnen
Umkugel- und Kantenradius
5. Vollständiges abgeschrägtes Dodekaeder
Ein komplexer archimedischer Körper mit perfekter mathematischer Harmonie
Das abgeschrägte Dodekaeder: Komplexität in der Polyedergeometrie
Das abgeschrägte Dodekaeder (englisch: Snub Dodecahedron) ist einer der komplexesten und faszinierendsten archimedischen Körper. Als einer von nur 13 uniform-konvexen Polyedern vereint er mathematische Eleganz mit struktureller Komplexität und demonstriert die tiefe Verbindung zwischen dem goldenen Schnitt und dreidimensionaler Geometrie.
Definition und fundamentale Struktur
Das abgeschrägte Dodekaeder entsteht durch eine spezielle geometrische Operation:
- Abschrägung (Snubbing): Aus einem regulären Dodekaeder durch gleichzeitiges Abstumpfen und Drehen
- 92 Flächen: 12 regelmäßige Fünfecke (vom ursprünglichen Dodekaeder) und 80 neue gleichseitige Dreiecke
- 150 Kanten: Alle mit identischer Länge, was den Körper zu einem archimedischen Polyeder macht
- 60 Ecken: Jede wird von genau 4 Dreiecken und 1 Fünfeck gebildet (Notation: 3.3.3.3.5)
- Chiralität: Existiert in zwei spiegelbildlichen Formen (Rechts- und Linkshänder)
Der goldene Schnitt als geometrisches Prinzip
Das abgeschrägte Dodekaeder ist eng mit dem goldenen Schnitt φ verknüpft:
Mathematische Grundlage
φ = (1+√5)/2 ≈ 1.618034 ist nicht nur eine mathematische Curiosität, sondern das fundamentale Verhältnis, das die Proportionen des abgeschrägten Dodekaeders bestimmt. Alle charakteristischen Größen lassen sich über φ ausdrücken.
Ikosaedrische Verwandtschaft
Die 60 Ecken des abgeschrägten Dodekaeders entsprechen den 60 Ecken eines Ikosaeders. Diese Verbindung zur ikosaedrischen Symmetriegruppe I_h verleiht dem Körper seine außergewöhnlichen Symmetrieeigenschaften.
Trigonometrische Komplexität
Der Parameter t ≈ 0.4716 entsteht aus einer kubischen Gleichung und beschreibt den Kosinus des Zentriwinkels im Sehnenfünfeck. Diese Größe ist essentiell für alle Volumen- und Radiusberechnungen.
Konstruktive Herausforderung
Die exakte Konstruktion mit Zirkel und Lineal ist unmöglich, da die Bestimmung von t die Lösung einer nicht-konstruierbaren kubischen Gleichung erfordert. Dies unterscheidet es von einfacheren Polyedern.
Symmetrie und Chiralität
Die Symmetrieeigenschaften des abgeschrägten Dodekaeders sind bemerkenswert:
Ikosaedrische Symmetriegruppe
Mit 60 Symmetrieoperationen (120 bei Einschluss der Spiegelungen) gehört das abgeschrägte Dodekaeder zur höchsten Symmetrieklasse unter den Polyedern. Diese Symmetrie erklärt seine ästhetische Perfektion.
Enantiomorphie
Die beiden chiralen Formen können nicht durch Rotation ineinander überführt werden. Diese Händigkeit ist ein seltenes Phänomen in der Polyedergeometrie und macht jede Form zu einem eigenständigen geometrischen Objekt.
Duale Beziehungen
Das abgeschrägte Dodekaeder ist selbst-dual in dem Sinne, dass sein dualer Körper (Pentagonal Hexecontahedron) dieselbe Symmetriegruppe besitzt, aber aus 60 Deltoid-Flächen besteht.
Rotationsachsen
Es besitzt 6 fünfzählige, 10 dreizählige und 15 zweizählige Rotationsachsen. Diese komplexe Symmetriestruktur macht es zu einem idealen Studienobjekt für Kristallographie und Gruppentheorie.
Anwendungen in Wissenschaft und Technik
Die praktische Bedeutung des abgeschrägten Dodekaeders erstreckt sich über die reine Mathematik hinaus:
- Kristallographie: Quasikristalle und ikosaedrische Phasen zeigen Strukturen, die dem abgeschrägten Dodekaeder verwandt sind
- Molekularchemie: Fullerene und große Kohlenstoff-Cluster können näherungsweise diese Geometrie aufweisen
- Virusforschung: Bestimmte Viruskapside nutzen ikosaedrische Symmetrien, die strukturelle Ähnlichkeiten aufweisen
- Architektur: Geodätische Kuppeln und Tensegrity-Strukturen verwenden verwandte Prinzipien
- Optik: Facettierte optische Elemente und Photonik-Kristalle nutzen ähnliche Symmetrien
- Spieltheorie: Als 92-seitiger "Würfel" für komplexe Zufallsgeneratoren
Beziehung zu anderen Polyedern
Das abgeschrägte Dodekaeder steht in einem reichen Beziehungsgeflecht zu anderen geometrischen Objekten:
Archimedische Familie
Als eines von 13 archimedischen Polyedern teilt es mit seinen Verwandten die Eigenschaft, aus regulären Polygonen zusammengesetzt zu sein, wobei jede Ecke identisch ist.
Dodekaeder-Verwandtschaft
Durch die Abschrägungsoperation entsteht es aus dem regulären Dodekaeder. Diese Transformation zeigt, wie komplexe Formen aus einfacheren hervorgehen können.
Ikosaeder-Analogie
Die gleiche Anzahl von Ecken und die ikosaedrische Symmetrie verbinden es eng mit dem Ikosaeder, einem der fünf platonischen Körper.
Dimension und Verallgemeinerung
In höheren Dimensionen gibt es analoge Strukturen (4D-Polytope), die ähnliche Symmetrie- und Komplexitätseigenschaften aufweisen.
Zusammenfassung
Das abgeschrägte Dodekaeder repräsentiert einen Höhepunkt geometrischer Komplexität und mathematischer Eleganz. Seine 92 Flächen, verbunden durch den goldenen Schnitt und ikosaedrische Symmetrie, machen es zu einem faszinierenden Studienobjekt für Mathematiker, Kristallographen und Künstler gleichermaßen. Die Chiralität verleiht ihm eine zusätzliche Dimension der Komplexität, während seine praktischen Anwendungen von der Nanotechnologie bis zur Architektur reichen. Als Brücke zwischen der Einfachheit platonischer Körper und der Komplexität moderner geometrischer Strukturen verkörpert das abgeschrägte Dodekaeder die Schönheit mathematischer Harmonie in ihrer vielleicht anspruchsvollsten Form. In einer Zeit, in der komplexe Systeme zunehmend wichtiger werden, bleibt es ein zeitloses Symbol für die Kraft geometrischer Prinzipien und mathematischer Präzision.