Kuboktaederstumpf berechnen
Rechner und Formeln zur Berechnung des Kuboktaederstumpfs (Truncated Cuboctahedron)
Kuboktaederstumpf Rechner
Der Kuboktaederstumpf
Ein Kuboktaederstumpf ist ein großer Rhombenkuboktaeder mit 26 Flächen: 12 Quadrate, 8 regelmäßige Sechsecke und 6 regelmäßige Achtecke.
Komplexe Struktur
Ein Kuboktaederstumpf ist ein großer Rhombenkuboktaeder.
Entsteht durch Abstumpfung des Kuboktaeders.
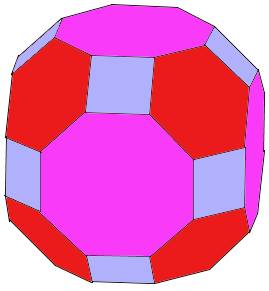
● 12 Quadrate ● 8 Sechsecke ● 6 Achtecke
|
|
Was ist ein Kuboktaederstumpf?
Ein Kuboktaederstumpf (Truncated Cuboctahedron oder Großer Rhombenkuboktaeder) ist ein komplexer archimedischer Körper:
- 26 Flächen: 12 Quadrate, 8 regelmäßige Sechsecke, 6 regelmäßige Achtecke
- 48 Ecken: Jede Ecke wird von 1 Quadrat, 1 Sechseck und 1 Achteck gebildet
- 72 Kanten: Alle Kanten haben die gleiche Länge
- Komplexe Abstumpfung: Entsteht durch Abstumpfung des Kuboktaeders
- Oktaedrische Symmetrie: 24 Symmetrieoperationen
- √2-Beziehungen: Proportionen basieren auf √2
Geometrische Eigenschaften
Der Kuboktaederstumpf besitzt komplexe geometrische Eigenschaften:
Flächenstruktur
- 12 Quadrate: Reguläre viereckige Flächen
- 8 Sechsecke: Regelmäßige sechseckige Flächen
- 6 Achtecke: Regelmäßige achteckige Flächen
- Vertex-Figur: Jede Ecke: 1 Quadrat + 1 Sechseck + 1 Achteck
Besondere Eigenschaften
- Oktaedrische Symmetrie: 24 Symmetrieoperationen
- √2 und √3 Konstanten: Komplexe mathematische Beziehungen
- Großer Rhombenkuboktaeder: Alternative Bezeichnung
- Duale Beziehung: Dual zu einem katalanischen Körper
Mathematische Beziehungen
Der Kuboktaederstumpf folgt komplexen mathematischen Gesetzen:
Volumenberechnung
Komplexe Formel mit √2, charakteristisch für oktaedrische Geometrie.
Oberflächenberechnung
Die Oberfläche kombiniert drei verschiedene regelmäßige Polygontypen.
Anwendungen des Kuboktaederstumpfs
Kuboktaederstümpfe finden sich in spezialisierten Bereichen:
Wissenschaft & Forschung
- Komplexe Kristallstrukturen
- Koordinationsgeometrie in der Chemie
- Materialwissenschaft und Metamaterialien
- Topologische Studien
Kunst & Design
- Avantgarde-Skulpturen
- Komplexe architektonische Elemente
- High-End Schmuckdesign
- 3D-Visualisierung und Rendering
Spiele & Simulation
- Komplexe Gaming-Würfel
- Virtual Reality Objekte
- Mathematische Puzzle
- CAD-Herausforderungen
Technik & Engineering
- Präzisions-Maschinenbau
- Komplexe optische Systeme
- Robotik und Automatisierung
- Aerospace-Komponenten
Formeln für den Kuboktaederstumpf
Volumen V
Komplexe Formel mit √2-Beziehungen
Oberfläche S
Kombiniert Quadrate, Sechsecke und Achtecke
Umkugelradius rc
Radius der umschreibenden Kugel
Kantenradius rm
Radius der Kugel durch Kantenmittelpunkte
√2-Konstante
Fundamentale Konstante in allen Formeln
√3-Konstante
Wichtige Konstante in Oberflächenformel
Rechenbeispiel für einen Kuboktaederstumpf
Gegeben
Gesucht: Alle Eigenschaften des Kuboktaederstumpfs
1. Konstanten berechnen
Fundamentale Konstanten bestimmen
2. Oberflächenberechnung
Oberfläche mit komplexer Formel
3. Volumenberechnung
Großes Volumen mit √2-Formel
4. Radien berechnen
Komplexe Radiusbeziehungen
5. Vollständiger Kuboktaederstumpf
Ein komplexer archimedischer Körper mit großer Oberfläche und oktaedrischer Symmetrie
Der Kuboktaederstumpf: Großer Rhombenkuboktaeder
Der Kuboktaederstumpf (englisch: Truncated Cuboctahedron, auch Great Rhombicuboctahedron genannt) steht als eindrucksvolles Beispiel für die Komplexität archimedischer Geometrie. Als einer der größeren und komplexeren gleichmäßigen Polyeder verkörpert er die fortgeschrittene mathematische Eleganz, die entsteht, wenn einfache geometrische Operationen auf bereits komplexe Grundformen angewendet werden. Mit seinen 26 Flächen aus drei verschiedenen regulären Polygontypen demonstriert er eindrucksvoll die Vielfalt und Schönheit der archimedischen Familie.
Die Abstumpfung des Kuboktaeders
Der Kuboktaederstumpf entsteht durch eine systematische geometrische Transformation:
- Ausgangsform: Kuboktaeder mit 14 Flächen (8 Dreiecke + 6 Quadrate)
- Abstumpfungsoperation: Systematisches Abschneiden aller Ecken des Kuboktaeders
- Flächentransformation: Dreiecke werden zu Sechsecken, Quadrate bleiben Quadrate
- Neue Flächen: An jeder abgeschnittenen Ecke entsteht ein regelmäßiges Achteck
- Flächenverteilung: 12 Quadrate + 8 Sechsecke + 6 Achtecke = 26 Flächen total
- Vertex-Konfiguration: (4.6.8) - an jeder Ecke treffen ein Quadrat, ein Sechseck und ein Achteck zusammen
Mathematische Komplexität und Eleganz
Der Kuboktaederstumpf zeigt bemerkenswerte mathematische Eigenschaften:
Komplexe Konstanten
Die Formeln enthalten sowohl √2 als auch √3, was auf die dualen Ursprünge aus kubischer und oktaedrischer Geometrie hinweist. Diese Kombination führt zu reichhaltigen mathematischen Beziehungen.
Große Zahlenwerte
Mit Faktoren wie (11+7√2) im Volumen und (2+√2+√3) in der Oberfläche zeigt er größere numerische Werte als einfachere archimedische Körper, was seine erhöhte Komplexität widerspiegelt.
Oktaedrische Symmetrie
Trotz seiner Komplexität behält er die oktaedrische Symmetriegruppe O_h bei, was seine Verwandtschaft mit Würfel, Oktaeder und Kuboktaeder unterstreicht.
Konstruktive Herausforderung
Die Konstruktion erfordert präzise Berechnungen. Die 26 Flächen müssen exakt ausgerichtet sein, um die gleichmäßige Eigenschaft zu bewahren.
Strukturelle Eigenschaften und Charakteristika
Der Kuboktaederstumpf zeigt einzigartige strukturelle Merkmale:
Duales Polyeder
Das duale Polyeder ist ein katalanischer Körper mit 48 Flächen. Diese hohe Flächenzahl des Duals spiegelt die Komplexität des ursprünglichen Polyeders wider.
Große Oberfläche
Mit 26 Flächen besitzt er eine der größten Oberflächen unter den archimedischen Körpern, was ihn für Anwendungen interessant macht, die große Oberflächenbereiche benötigen.
Euler-Charakteristik
Mit V = 48, E = 72, F = 26 erfüllt er perfekt Eulers Polyederformel: V - E + F = 2. Die hohen Zahlen zeigen seine strukturelle Komplexität.
Drei Polygontypen
Die Kombination aus Quadraten, Sechsecken und Achtecken macht ihn zu einem der vielfältigsten archimedischen Körper in Bezug auf Flächentypen.
Anwendungen und praktische Bedeutung
Der Kuboktaederstumpf findet vielfältige Anwendungen:
- Kristallographie: Modell für komplexe Kristallstrukturen mit mehreren Koordinationstypen
- Architektur: Inspiration für komplexe Kuppel- und Raumstrukturen
- Molekularchemie: Template für große Käfigmoleküle und Koordinationskomplexe
- Materialwissenschaft: Grundlage für Metamaterialien mit komplexen optischen Eigenschaften
- 3D-Design: Herausforderung für fortgeschrittene CAD-Anwendungen
- Mathematische Bildung: Beispiel für fortgeschrittene Polyeder-Theorie
- Kunst und Skulptur: Grundlage für komplexe geometrische Kunstwerke
- Gaming: Basis für spezielle Würfel und komplexe Spielkomponenten
Historische und kulturelle Einordnung
Der Kuboktaederstumpf hat eine besondere Stellung in der Geometriegeschichte:
Archimedische Tradition
Als einer der 13 archimedischen Körper steht er in der Tradition antiker griechischer Geometrie, zeigt aber bereits die Komplexität, die über die einfachen platonischen Körper hinausgeht.
Moderne Relevanz
In der modernen Mathematik und Physik dient er als Beispiel für komplexe Symmetrien und als Testfall für neue geometrische Theorien und Algorithmen.
Pädagogischer Wert
Er demonstriert, wie aus einfachen Operationen (Abstumpfung) hochkomplexe und dennoch harmonische Strukturen entstehen können - ein wichtiges Konzept in Mathematik und Naturwissenschaften.
Symbolische Bedeutung
Er steht symbolisch für die Idee, dass Komplexität und Ordnung sich nicht ausschließen, sondern zu höherer Schönheit führen können.
Zusammenfassung
Der Kuboktaederstumpf verkörpert die fortgeschrittene Eleganz archimedischer Geometrie und zeigt eindrucksvoll, wie systematische mathematische Operationen zu Strukturen von beeindruckender Komplexität und Schönheit führen können. Seine 26 Flächen, orchestriert durch die mathematischen Konstanten √2 und √3, machen ihn zu einem faszinierenden Studienobjekt für Mathematiker, Architekten und Künstler gleichermaßen. Als großer Rhombenkuboktaeder steht er für die Idee, dass wahre geometrische Schönheit oft in der intelligenten Kombination vielfältiger Elemente zu finden ist. Von antiken geometrischen Studien bis zu modernen technischen Anwendungen bleibt er ein zeitloses Beispiel für die Kraft mathematischer Ordnung und die unendlichen Möglichkeiten, die sich eröffnen, wenn Einfachheit und Komplexität in harmonischer Balance stehen. In einer Zeit zunehmender technischer Sophistikation erinnert er uns daran, dass die elegantesten Lösungen oft aus der systematischen Anwendung grundlegender Prinzipien auf komplexe Herausforderungen entstehen.