Oktaederstumpf berechnen
Rechner und Formeln zur Berechnung des Oktaederstumpfs (Truncated Octahedron)
Oktaederstumpf Rechner
Der Oktaederstumpf
Ein Oktaederstumpf ist ein gleichmäßiger Körper mit 14 Flächen: 6 Quadrate und 8 regelmäßige Sechsecke - entsteht durch Abstumpfung des Oktaeders.
Oktaederstumpf-Struktur
Ein Oktaederstumpf entsteht durch Abstumpfung des Oktaeders.
Alle Ecken werden gleichmäßig abgeschnitten.
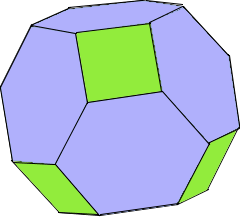
● 6 Quadrate ● 8 Sechsecke ● 24 Ecken
|
|
Was ist ein Oktaederstumpf?
Ein Oktaederstumpf (Truncated Octahedron) ist ein eleganter archimedischer Körper:
- 14 Flächen: 6 Quadrate und 8 regelmäßige Sechsecke
- 24 Ecken: Jede Ecke wird von 1 Quadrat und 2 Sechsecken gebildet
- 36 Kanten: Alle Kanten haben die gleiche Länge
- Oktaedrische Abstumpfung: Entsteht durch Abstumpfung des Oktaeders
- Oktaedrische Symmetrie: 24 Symmetrieoperationen
- √2-Beziehungen: Einfache mathematische Verhältnisse
Geometrische Eigenschaften
Der Oktaederstumpf besitzt elegante geometrische Eigenschaften:
Flächenstruktur
- 6 Quadrate: Entstehen aus den ursprünglichen Oktaeder-Flächen
- 8 Sechsecke: Entstehen an den abgeschnittenen Ecken
- Einheitliche Kanten: Alle 36 Kanten sind gleich lang
- Vertex-Figur: Jede Ecke: 1 Quadrat + 2 Sechsecke
Besondere Eigenschaften
- Oktaedrische Symmetrie: 24 Symmetrieoperationen
- Einfache Konstanten: Hauptsächlich √2 und √3
- Raumfüllung: Füllt den Raum perfekt aus (Tessellation)
- Duale Beziehung: Dual zum tetragonalen Deltoeder
Mathematische Beziehungen
Der Oktaederstumpf folgt eleganten mathematischen Gesetzen:
Volumenberechnung
Sehr einfache Formel mit √2, charakteristisch für oktaedrische Geometrie.
Oberflächenberechnung
Die Oberfläche kombiniert die Flächen von Quadraten und Sechsecken.
Anwendungen des Oktaederstumpfs
Oktaederstümpfe finden sich in vielen Bereichen:
Wissenschaft & Forschung
- Raumfüllende Strukturen in der Kristallographie
- Koordinationsgeometrie in der Chemie
- Materialwissenschaft und Packungsprobleme
- Biologie: Zellanordnungen und Wabenstrukturen
Kunst & Design
- Architektonische Raumstrukturen
- Skulpturen und moderne Kunst
- Tessellationsdesign und Muster
- Industriedesign und Verpackungen
Spiele & Simulation
- 14-seitige Würfel für Tabletop-Spiele
- Puzzle und mechanische Spielzeuge
- Virtual Reality und 3D-Grafik
- Mathematische Lernspiele
Technik & Engineering
- Maschinenbau: Effiziente Raumnutzung
- Robotik und Automatisierung
- Optische Systeme und Prismen
- Aerospace: Leichtbaustrukturen
Formeln für den Oktaederstumpf
Volumen V
Sehr einfache Formel mit √2-Beziehung
Oberfläche S
Kombiniert Quadrate und Sechsecke
Umkugelradius rc
Radius der umschreibenden Kugel
Kantenradius rm
Sehr einfache rationale Beziehung
√2-Konstante
Fundamentale Konstante in Volumenformel
√3-Konstante
Konstante in Oberflächenformel
Rechenbeispiel für einen Oktaederstumpf
Gegeben
Gesucht: Alle Eigenschaften des Oktaederstumpfs
1. Konstanten berechnen
Fundamentale Konstanten bestimmen
2. Oberflächenberechnung
Oberfläche mit √3-Faktor
3. Volumenberechnung
Großes Volumen mit √2-Formel
4. Radien berechnen
Einfache Radiusbeziehungen
5. Vollständiger Oktaederstumpf
Ein eleganter archimedischer Körper mit raumfüllenden Eigenschaften und oktaedrischer Symmetrie
Der Oktaederstumpf: Eleganz der oktaedrischen Abstumpfung
Der Oktaederstumpf (englisch: Truncated Octahedron) steht als herausragendes Beispiel für die Eleganz und praktische Bedeutung archimedischer Geometrie. Als einer der wichtigsten und vielseitigsten gleichmäßigen Polyeder verkörpert er die perfekte Balance zwischen mathematischer Schönheit und praktischer Anwendbarkeit. Mit seinen 14 Flächen - 6 Quadraten und 8 regelmäßigen Sechsecken - demonstriert er eindrucksvoll, wie aus der systematischen Modifikation eines platonischen Körpers Strukturen von außergewöhnlicher Vielseitigkeit entstehen können.
Die Abstumpfung des Oktaeders
Der Oktaederstumpf entsteht durch eine elegante geometrische Transformation:
- Ausgangsform: Reguläres Oktaeder mit 8 dreieckigen Flächen und 6 Ecken
- Abstumpfungsoperation: Systematisches Abschneiden aller 6 Ecken des Oktaeders
- Flächentransformation: Jede ursprüngliche Dreiecksfläche wird zu einem Sechseck
- Neue Flächen: An jeder abgeschnittenen Ecke entsteht ein Quadrat
- Flächenverteilung: 8 Sechsecke + 6 Quadrate = 14 Flächen total
- Vertex-Konfiguration: (4.6.6) - an jeder Ecke treffen ein Quadrat und zwei Sechsecke zusammen
Mathematische Eleganz und Einfachheit
Der Oktaederstumpf besticht durch seine mathematische Klarheit:
Einfache Formeln
Mit V = 8√2a³ und S = 6a²(1+2√3) besitzt er überraschend einfache und elegante Formeln. Diese mathematische Klarheit macht ihn ideal für Berechnungen und theoretische Studien.
Raumfüllende Eigenschaft
Als einer der wenigen Polyeder kann der Oktaederstumpf den dreidimensionalen Raum vollständig und lückenlos füllen (Tessellation). Diese Eigenschaft macht ihn extrem wertvoll für praktische Anwendungen.
Oktaedrische Symmetrie
Mit 24 Symmetrieoperationen behält er die volle oktaedrische Symmetriegruppe O_h bei, was seine Verwandtschaft zum ursprünglichen Oktaeder unterstreicht.
Rationale Beziehungen
Der Kantenradius r_m = 3a/2 zeigt eine besonders einfache rationale Beziehung, die in der Polyeder-Geometrie selten ist und den Oktaederstumpf auszeichnet.
Raumfüllung und strukturelle Eigenschaften
Der Oktaederstumpf zeigt einzigartige strukturelle Merkmale:
Raumfüllende Tessellation
Oktaederstümpfe können den gesamten Raum ohne Lücken oder Überlappungen füllen. Diese Eigenschaft teilen nur wenige Polyeder und macht sie extrem wertvoll für Packungsprobleme.
Strukturelle Stabilität
Die Kombination aus Quadraten und Sechsecken verleiht optimale strukturelle Eigenschaften. Die Form ist selbsttragend und mechanisch robust.
Duales Polyeder
Das duale Polyeder zum Oktaederstumpf ist das tetragonale Deltoeder mit 24 Flächen. Diese Dualität verbindet archimedische und katalanische Körper.
Optimale Raumnutzung
Mit einem Verhältnis von Oberfläche zu Volumen, das nahe dem optimalen liegt, eignet er sich hervorragend für effiziente Raumnutzung.
Praktische Anwendungen und moderne Relevanz
Der Oktaederstumpf findet vielfältige praktische Anwendungen:
- Kristallographie: Natürliche Kristallformen und synthetische Materialien
- Architektur: Raumfüllende Strukturen und modulare Bauweise
- Verpackungsindustrie: Optimale Raumnutzung und Materialeffizienz
- Materialwissenschaft: Schaumstrukturen und leichte Materialien
- Biologie: Zellanordnungen und natürliche Packungsstrukturen
- Gaming: 14-seitige Würfel für Tabletop-Spiele
- 3D-Grafik: Grundform für Subdivision-Algorithmen
- Robotik: Modulare Robotersysteme und Schwarmroboter
Historische und kulturelle Bedeutung
Der Oktaederstumpf hat eine besondere Stellung in der Geometriegeschichte:
Archimedische Tradition
Als einer der 13 archimedischen Körper steht er in der direkten Nachfolge antiker griechischer Geometrie und zeigt, wie systematische Operationen zu neuen, wertvollen Strukturen führen.
Industrielle Revolution
Mit der Industrialisierung gewann der Oktaederstumpf an Bedeutung für effiziente Packung und Materialnutzung. Seine raumfüllenden Eigenschaften wurden für praktische Probleme nutzbar.
Moderne Wissenschaft
In der modernen Materialwissenschaft und Nanotechnologie dient er als Modell für effiziente Strukturen und optimierte Raumnutzung.
Symbolische Bedeutung
Er steht symbolisch für die Idee, dass durch intelligente Modifikation einfacher Grundformen Strukturen von größerer Vielseitigkeit und praktischer Bedeutung entstehen können.
Zusammenfassung
Der Oktaederstumpf verkörpert die perfekte Synthese aus mathematischer Eleganz und praktischer Anwendbarkeit. Seine einfachen Formeln und raumfüllenden Eigenschaften machen ihn zu einem der wertvollsten Polyeder in der angewandten Geometrie. Von kristallographischen Strukturen bis zu modernen Verpackungslösungen zeigt er, wie fundamentale geometrische Prinzipien praktische Probleme lösen können. Seine 14 Flächen, orchestriert durch die eleganten Konstanten √2 und √3, demonstrieren die Kraft systematischer geometrischer Operationen. Als Oktaederstumpf steht er für die Idee, dass wahre geometrische Schönheit oft in der intelligenten Vereinfachung und Optimierung liegt. In einer Zeit zunehmender Ressourcenknappheit und Effizienzanforderungen bleibt er ein zeitloses Beispiel für die Kraft mathematischer Ordnung und die praktische Anwendbarkeit geometrischer Prinzipien. Als eleganter Vermittler zwischen platonischer Reinheit und archimedischer Vielseitigkeit repräsentiert er das Beste aus beiden Welten.