Rhombenikosidodekaeder berechnen
Rechner und Formeln zur Berechnung des Rhombenikosidodekaeders (Rhombicosidodecahedron)
Rhombenikosidodekaeder Rechner
Das Rhombenikosidodekaeder
Ein Rhombenikosidodekaeder ist ein eleganter archimedischer Körper mit 62 Flächen: 20 gleichseitige Dreiecke, 30 Quadrate und 12 regelmäßige Fünfecke.
Ikosaedrische Eleganz
Ein Rhombenikosidodekaeder vereint drei Polygontypen.
Elegante ikosaedrische Symmetrie mit 62 Flächen.
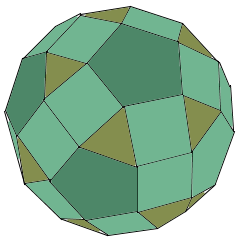
● 20 Dreiecke ● 30 Quadrate ● 12 Fünfecke
|
|
Was ist ein Rhombenikosidodekaeder?
Ein Rhombenikosidodekaeder (Rhombicosidodecahedron) ist ein eleganter archimedischer Körper:
- 62 Flächen: 20 gleichseitige Dreiecke, 30 Quadrate, 12 regelmäßige Fünfecke
- 120 Ecken: Jede Ecke wird von 1 Dreieck, 1 Quadrat und 1 Fünfeck gebildet
- 180 Kanten: Alle Kanten haben die gleiche Länge
- Ikosaedrische Symmetrie: Höchste Symmetriegruppe mit 60 Operationen
- Goldener Schnitt: Proportionen basieren auf φ = (1+√5)/2
- Drei Polygontypen: Einzigartige Kombination von Formen
Geometrische Eigenschaften
Das Rhombenikosidodekaeder besitzt faszinierende geometrische Eigenschaften:
Flächenstruktur
- 20 Dreiecke: Gleichseitige dreieckige Flächen
- 30 Quadrate: Regelmäßige viereckige Flächen
- 12 Fünfecke: Regelmäßige fünfeckige Flächen
- Vertex-Figur: Jede Ecke: 1 Dreieck + 1 Quadrat + 1 Fünfeck
Besondere Eigenschaften
- Ikosaedrische Symmetrie: 60 Symmetrieoperationen
- Goldener Schnitt: φ = (1+√5)/2 ≈ 1.618
- Kleiner Rhombenkuboktaeder: Alternative Bezeichnung
- Quasi-reguläre Eigenschaft: Hohe Symmetrie
Mathematische Beziehungen
Das Rhombenikosidodekaeder folgt eleganten mathematischen Gesetzen:
Volumenberechnung
Komplexe Formel mit √5, charakteristisch für ikosaedrische Geometrie.
Oberflächenberechnung
Die Oberfläche kombiniert drei verschiedene regelmäßige Polygontypen.
Anwendungen des Rhombenikosidodekaeders
Rhombenikosidodekaeder finden sich in verschiedenen Bereichen:
Wissenschaft & Forschung
- Komplexe Molekülstrukturen und Fullerene
- Koordinationsgeometrie in der Chemie
- Kristallographie und Materialwissenschaft
- Topologische Studien in der Mathematik
Kunst & Design
- Skulpturen und moderne Kunst
- Architektonische Kuppelstrukturen
- Schmuckdesign und Edelsteinschliff
- Industriedesign und Produktgestaltung
Spiele & Unterhaltung
- Komplexe Würfel für Sammler
- Puzzle und mechanische Spielzeuge
- 3D-Modellierung und Animation
- Virtual Reality Anwendungen
Technik & Engineering
- Strukturoptimierung und Leichtbau
- Geodätische Strukturen
- Antennentechnik und Satelliten
- Optische Systeme und Prismen
Formeln für das Rhombenikosidodekaeder
Volumen V
Komplexe Formel mit √5-Beziehungen
Oberfläche S
Kombiniert Dreiecke, Quadrate und Fünfecke
Umkugelradius rc
Radius der umschreibenden Kugel
Kantenradius rm
Radius der Kugel durch Kantenmittelpunkte
Goldener Schnitt φ
Fundamentale Konstante in allen Formeln
√3-Konstante
Wichtige Konstante in Oberflächenformel
Rechenbeispiel für ein Rhombenikosidodekaeder
Gegeben
Gesucht: Alle Eigenschaften des Rhombenikosidodekaeders
1. Goldener Schnitt
Fundamentale Konstanten berechnen
2. Oberflächenberechnung
Große Oberfläche durch 62 Flächen
3. Volumenberechnung
Großes Volumen mit φ-Faktoren
4. Radien berechnen
Komplexe φ-abhängige Radien
5. Vollständiges Rhombenikosidodekaeder
Ein eleganter archimedischer Körper mit ikosaedrischer Symmetrie und goldenem Schnitt
Das Rhombenikosidodekaeder: Ikosaedrische Eleganz
Das Rhombenikosidodekaeder (englisch: Rhombicosidodecahedron, auch Small Rhombicosidodecahedron genannt) steht als faszinierendes Beispiel für die Vereinigung verschiedener geometrischer Formen zu einer harmonischen Einheit. Als einer der elegantesten archimedischen Körper verkörpert es die Schönheit ikosaedrischer Symmetrie und demonstriert eindrucksvoll, wie drei verschiedene reguläre Polygontypen - Dreiecke, Quadrate und Fünfecke - in perfekter mathematischer Harmonie koexistieren können. Seine 62 Flächen machen ihn zu einem der komplexeren gleichmäßigen Polyeder und gleichzeitig zu einem der ästhetisch ansprechendsten.
Die ikosaedrische Familie
Das Rhombenikosidodekaeder gehört zur ikosaedrischen Familie der archimedischen Körper:
- Ikosaedrische Symmetrie: Besitzt die höchste Rotationssymmetrie mit 60 Symmetrieoperationen
- Goldener Schnitt: Alle Proportionen basieren auf φ = (1+√5)/2 ≈ 1.618
- Quasi-reguläre Eigenschaft: Hohe Uniformität trotz verschiedener Flächentypen
- Drei Polygontypen: 20 Dreiecke + 30 Quadrate + 12 Fünfecke = 62 Flächen
- Vertex-Konfiguration: (3.4.5.4) - an jeder Ecke alternierend
- Verwandtschaft: Eng verwandt mit Ikosaeder und Dodekaeder
Mathematische Schönheit und Komplexität
Das Rhombenikosidodekaeder vereint mathematische Eleganz mit struktureller Komplexität:
Goldener Schnitt Allgegenwärtig
Der goldene Schnitt φ durchdringt alle Formeln und Proportionen. Von den Radiusbeziehungen bis zu den Flächenanordnungen - überall finden sich die charakteristischen √5-Ausdrücke.
Komplexe aber elegante Formeln
Trotz der Komplexität mit verschachtelten Wurzelausdrücken zeigen die Formeln eine innere Logik und Schönheit, die die mathematische Harmonie des Körpers widerspiegelt.
Maximale Symmetrie
Mit der ikosaedrischen Symmetriegruppe I_h besitzt es die höchstmögliche Rotationssymmetrie. Diese Symmetrie verleiht ihm seine außergewöhnliche ästhetische Wirkung.
Strukturelle Perfektion
Die Anordnung der 62 Flächen folgt strengen mathematischen Gesetzen. Jede Abweichung würde die Uniformität zerstören und einen anderen Polyedertyp erzeugen.
Konstruktion und geometrische Verwandtschaften
Das Rhombenikosidodekaeder zeigt faszinierende Beziehungen zu anderen Polyedern:
Archimedische Verwandtschaft
Es kann als "erweiterte" Version des Ikosidodekaeders betrachtet werden, bei dem zusätzliche Flächen eingefügt wurden, ohne die grundlegende ikosaedrische Struktur zu zerstören.
Konstruktive Herausforderung
Die exakte Konstruktion erfordert präzise Berechnungen der Winkel und Proportionen. Bereits kleine Fehler führen zu ungleichen Kantenlängen.
Dualität
Das duale Polyeder ist ein komplexer katalanischer Körper mit 120 Flächen, was die hohe Symmetrie des ursprünglichen Polyeders unterstreicht.
Modulare Struktur
Die drei Flächentypen sind nicht zufällig verteilt, sondern folgen einem strengen modularen System, das die ikosaedrische Symmetrie erhält.
Praktische Anwendungen und moderne Relevanz
Das Rhombenikosidodekaeder findet vielfältige praktische Anwendungen:
- Fullerene-Chemie: Modell für komplexe Kohlenstoffstrukturen und Nanomaterialien
- Architektur: Inspiration für geodätische Kuppeln und komplexe Raumstrukturen
- Kristallographie: Modell für Quasikristalle und komplexe Kristallstrukturen
- Optik: Grundlage für komplexe Prismensysteme und optische Instrumente
- Kunst und Design: Inspiration für Skulpturen und dekorative Objekte
- Gaming: Basis für spezielle Würfel und Sammlerobjekte
- Bildung: Exzellentes Beispiel für fortgeschrittene Polyeder-Theorie
- 3D-Grafik: Herausforderung für Rendering-Algorithmen
Kulturelle und historische Bedeutung
Das Rhombenikosidodekaeder hat eine reiche kulturelle Tradition:
Antike Wurzeln
Obwohl erst später formal beschrieben, verkörpert es die antike griechische Faszination für geometrische Perfektion und die Harmonie der Proportionen.
Renaissance-Ideal
In der Renaissance wurde es als Symbol für die Verbindung von Kunst und Mathematik geschätzt. Es zeigt, wie Schönheit aus mathematischer Ordnung entsteht.
Moderne Wissenschaft
In der modernen Physik und Chemie dient es als Modell für komplexe Symmetrien und als Testfall für neue Theorien über Struktur und Form.
Symbolische Bedeutung
Es steht symbolisch für die Idee, dass aus der intelligenten Kombination einfacher Elemente Strukturen von außergewöhnlicher Komplexität und Schönheit entstehen können.
Zusammenfassung
Das Rhombenikosidodekaeder verkörpert die Quintessenz archimedischer Eleganz und zeigt eindrucksvoll, wie verschiedene geometrische Formen zu einer harmonischen Einheit verschmelzen können. Seine 62 Flächen, orchestriert durch den goldenen Schnitt und die ikosaedrische Symmetrie, machen es zu einem Meisterwerk geometrischer Kunst. Von antiken philosophischen Betrachtungen bis zu modernen nanotechnologischen Anwendungen bleibt es ein zeitloses Symbol für die Kraft mathematischer Harmonie. Als Brücke zwischen der Reinheit platonischer Formen und der Vielfalt archimedischer Kreativität repräsentiert es das Beste aus beiden Welten. In einer Zeit zunehmender Komplexität erinnert es uns daran, dass wahre Schönheit oft in der intelligenten Organisation vielfältiger Elemente zu einer höheren Ordnung liegt. Seine drei Polygontypen stehen symbolisch für die Idee, dass Diversität und Einheit sich nicht ausschließen, sondern zu größerer Vollkommenheit führen können.