Dodekaederstumpf berechnen

Rechner und Formeln zur Berechnung des Dodekaederstumpfs (Truncated Dodecahedron)

Dodekaederstumpf Rechner

Der Dodekaederstumpf

Ein Dodekaederstumpf ist ein archimedischer Körper mit 32 Flächen: 20 gleichseitige Dreiecke und 12 regelmäßige Zehnecke.

Bekannten Parameter eingeben
Welcher Parameter ist bekannt?
Wert des ausgewählten Parameters
Dodekaederstumpf-Eigenschaften

Symmetrische Struktur: 60 Ecken, 90 Kanten, 32 Flächen

20 Dreiecke 12 Zehnecke Archimedisch
Dodekaederstumpf-Berechnungsergebnisse
Seitenlänge a:
Volumen V:
Oberfläche S:
Umkugelradius rc:
Kantenradius rm:

Dodekaederstumpf-Struktur

Ein Dodekaederstumpf ist ein archimedischer Körper.
Er entsteht durch Abstumpfung eines regulären Dodekaeders.

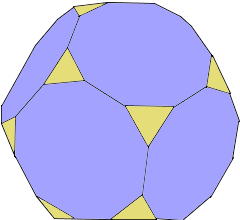
Dodekaederstumpf

● 20 Dreiecke ● 12 Zehnecke ● 60 Ecken

Was ist ein Dodekaederstumpf?

Ein Dodekaederstumpf (Truncated Dodecahedron) ist einer der 13 archimedischen Körper:

  • 32 Flächen: 20 gleichseitige Dreiecke und 12 regelmäßige Zehnecke
  • 60 Ecken: Jede Ecke wird von 2 Dreiecken und 1 Zehneck gebildet
  • 90 Kanten: Alle Kanten haben die gleiche Länge
  • Entstehung: Durch Abstumpfung eines regulären Dodekaeders
  • Ikosaedrische Symmetrie: Hohe Symmetriegruppe
  • Goldener Schnitt: Proportionen basieren auf φ

Geometrische Eigenschaften

Der Dodekaederstumpf besitzt faszinierende geometrische Eigenschaften:

Flächenstruktur
  • 20 Dreiecke: Gleichseitige dreieckige Flächen
  • 12 Zehnecke: Regelmäßige zehneckige Flächen
  • Einheitliche Kanten: Alle 90 Kanten sind gleich lang
  • Vertex-Figur: Jede Ecke: 2 Dreiecke + 1 Zehneck
Besondere Eigenschaften
  • Ikosaedrische Symmetrie: 60 Symmetrieoperationen
  • Goldener Schnitt: φ = (1+√5)/2 ≈ 1.618
  • Truncation: Entstanden durch Eckenabschnitt
  • Konvexer Körper: Alle Innenwinkel < 180°

Mathematische Beziehungen

Der Dodekaederstumpf folgt eleganten mathematischen Gesetzen:

Volumenberechnung
V = 5a³(99+47√5)/12

Das Volumen beinhaltet den goldenen Schnitt √5 und komplexe arithmetische Beziehungen.

Oberflächenberechnung
S = 5a²(√3 + 6√(5+2√5))

Die Oberfläche kombiniert die Flächen von Dreiecken und regelmäßigen Zehnecken.

Anwendungen des Dodekaederstumpfs

Dodekaederstümpfe finden sich in verschiedenen Bereichen:

Wissenschaft & Forschung
  • Fullerene und Carbon-Nanostrukturen
  • Kristallographie und Festkörperphysik
  • Viruskapside und biologische Symmetrien
  • Molekulare Käfigverbindungen
Kunst & Design
  • Architekturfußbälle und Sportbälle
  • Skulpturen und geometrische Installationen
  • Schmuckdesign und Ornamentik
  • 3D-Design und digitale Modellierung
Spiele & Unterhaltung
  • Fußbälle (klassische schwarz-weiße Muster)
  • Puzzle und mathematische Spielzeuge
  • Geodätische Kuppeln und Dome-Strukturen
  • Virtual Reality und 3D-Environments
Technik & Engineering
  • Druckbehälter und Strukturelemente
  • Optische Komponenten und Prismastrukturen
  • Antennendesign und Empfangsstrukturen
  • Biomedizinische Implantate

Formeln für den Dodekaederstumpf

Volumen V
\[V=\frac{5a^3(99+47\sqrt{5})}{12}\]

Komplex mit goldenem Schnitt-Beziehungen

Oberfläche S
\[S= 5a^2(\sqrt{3}+6\sqrt{5+2\sqrt{5}})\]

Kombiniert Dreiecks- und Zehneckflächen

Umkugelradius rc
\[r_c=\frac{a\sqrt{74+30\sqrt{5}}}{4}\]

Radius der umschreibenden Kugel

Kantenradius rm
\[r_m=\frac{a(5+3\sqrt{5})}{4}\]

Radius der Kugel durch Kantenmittelpunkte

Goldener Schnitt φ
\[\phi = \frac{1+\sqrt{5}}{2} \approx 1.618\]

Fundamentale Konstante in allen Formeln

Seitenlänge a
\[a = \sqrt{\frac{S}{5(\sqrt{3}+6\sqrt{5+2\sqrt{5}})}}\]

Aus anderen Parametern berechenbar

Rechenbeispiel für einen Dodekaederstumpf

Gegeben
Seitenlänge a = 10

Gesucht: Alle Eigenschaften des Dodekaederstumpfs

1. Goldener Schnitt
\[\phi = \frac{1+\sqrt{5}}{2} = 1.618034\] \[\sqrt{5} = 2.236068\]

Fundamentale Konstanten berechnen

2. Oberflächenberechnung
\[S = 5 \times 100 \times 15.529\] \[S = 7764.5\]

Oberfläche aus Seitenlänge

3. Volumenberechnung
\[V = \frac{5 \times 1000 \times 204.12}{12}\] \[V = 85050\]

Komplexe Volumenformel anwenden

4. Radien berechnen
\[r_c = 10 \times 2.785 = 27.85\] \[r_m = 10 \times 2.618 = 26.18\]

Umkugel- und Kantenradius

5. Vollständiger Dodekaederstumpf
Seitenlänge a = 10.00 Oberfläche S = 7764.5
Volumen V = 85050 Umkugelradius = 27.85
Kantenradius = 26.18 32 Flächen total

Ein eleganter archimedischer Körper mit ikosaedrischer Symmetrie

Der Dodekaederstumpf: Perfektion durch Abstumpfung

Der Dodekaederstumpf (englisch: Truncated Dodecahedron) ist einer der elegantesten archimedischen Körper und ein faszinierendes Beispiel dafür, wie durch eine systematische Transformation - die Abstumpfung - aus einem regulären platonischen Körper eine neue, komplexe und dennoch harmonische geometrische Form entstehen kann. Als Verbindung zwischen der Einfachheit des Dodekaeders und der Komplexität moderner geometrischer Strukturen verkörpert er mathematische Eleganz in ihrer reinsten Form.

Die Abstumpfungsoperation

Der Dodekaederstumpf entsteht durch eine präzise geometrische Transformation:

  • Ausgangsform: Reguläres Dodekaeder mit 12 regelmäßigen Fünfecken
  • Abstumpfung: Jede der 20 Ecken wird durch eine dreieckige Fläche ersetzt
  • Flächentransformation: Die 12 ursprünglichen Fünfecke werden zu regelmäßigen Zehnecken
  • Resultat: 20 neue gleichseitige Dreiecke + 12 regelmäßige Zehnecke = 32 Flächen
  • Kantenlänge: Der Abstumpfungsgrad wird so gewählt, dass alle 90 Kanten gleich lang sind

Der goldene Schnitt als geometrisches Prinzip

Wie sein Ursprung, das Dodekaeder, ist auch der Dodekaederstumpf eng mit dem goldenen Schnitt verknüpft:

Ikosaedrische Verwandtschaft

Der Dodekaederstumpf besitzt die gleiche ikosaedrische Symmetriegruppe I_h wie das ursprüngliche Dodekaeder. Diese Symmetrie umfasst 60 Rotationen und 60 Spiegelungen, insgesamt 120 Symmetrieoperationen.

Goldene Proportionen

Alle charakteristischen Maße des Dodekaederstumpfs lassen sich über den goldenen Schnitt φ = (1+√5)/2 ausdrücken. Die Zehnecke haben Seitenlängen und Diagonalen, die in goldenem Verhältnis stehen.

Komplexe Arithmetik

Die Formeln für Volumen und Oberfläche enthalten verschachtelte Wurzelausdrücke mit √5, die charakteristisch für ikosaedrische Geometrie sind. Diese Komplexität spiegelt die reiche geometrische Struktur wider.

Konstruktive Präzision

Die exakte Konstruktion erfordert präzise Berechnungen der Abstumpfungswinkel. Bereits kleine Abweichungen führen zu ungleichen Kantenlängen und zerstören die archimedische Eigenschaft.

Strukturelle und symmetrische Eigenschaften

Der Dodekaederstumpf zeigt bemerkenswerte strukturelle Eigenschaften:

Flächentypen und Winkel

Die 20 Dreiecke sind perfekt gleichseitig mit 60°-Winkeln. Die 12 Zehnecke sind regulär mit Innenwinkeln von 144°. An jeder Ecke treffen zwei Dreiecke und ein Zehneck zusammen (3.3.10).

Euler-Charakteristik

Mit V = 60, E = 90, F = 32 erfüllt der Dodekaederstumpf Eulers Polyederformel: V - E + F = 2. Diese topologische Eigenschaft gilt für alle konvexen Polyeder.

Duale Beziehungen

Das duale Polyeder zum Dodekaederstumpf ist das Triacis-Ikosaeder (Triakis Icosahedron), ein katalanischer Körper mit 60 unregelmäßigen dreieckigen Flächen.

Raumeffizienz

Der Dodekaederstumpf hat ein besonders günstiges Verhältnis von Volumen zu Oberfläche unter den archimedischen Körpern, was ihn für praktische Anwendungen interessant macht.

Praktische Anwendungen und kulturelle Bedeutung

Der Dodekaederstumpf findet vielfältige praktische Anwendungen:

  • Fußball-Design: Der klassische schwarz-weiße Fußball basiert auf dieser Geometrie (weiße Zehnecke, schwarze Dreiecke)
  • Fullerene-Chemie: Große Carbon-Fullerene können diese Struktur approximieren
  • Virus-Kapsid: Bestimmte Virusstrukturen nutzen ähnliche ikosaedrische Symmetrien
  • Geodätische Kuppeln: Buckminster Fuller verwendete verwandte Prinzipien
  • Kristallographie: Quasikristalle zeigen verwandte Symmetrieeigenschaften
  • Architektur: Kuppel- und Dachstrukturen nutzen die strukturelle Stabilität
  • Schmuckdesign: Die harmonischen Proportionen machen ihn ästhetisch ansprechend

Moderne Relevanz und Zukunftsperspektiven

In der modernen Wissenschaft und Technik gewinnt der Dodekaederstumpf neue Bedeutung:

Nanotechnologie

Nanostrukturen und molekulare Käfige nutzen die optimalen Packungseigenschaften. Die Kombination aus Stabilität und Zugänglichkeit macht ihn ideal für Wirkstofftransport.

3D-Druck und Fertigung

Moderne additive Fertigungsverfahren ermöglichen präzise Umsetzung komplexer Geometrien. CAD-Software berechnet automatisch alle Winkel und Dimensionen.

Materialwissenschaft

Metamaterialien und photonische Kristalle nutzen die einzigartigen Symmetrieeigenschaften für Anwendungen in Optik und Elektronik.

Biomimetik

Die in der Natur vorkommenden ikosaedrischen Strukturen inspirieren neue biomimetische Materialien und Konstruktionsprinzipien.

Zusammenfassung

Der Dodekaederstumpf vereint die Eleganz platonischer Geometrie mit der Komplexität archimedischer Transformation. Seine 32 Flächen, gesteuert durch den goldenen Schnitt und ikosaedrische Symmetrie, demonstrieren wie systematische geometrische Operationen zu ästhetisch ansprechenden und praktischen Anwendungen führen können. Von Sportbällen bis zu Nanostrukturen, von antiker Mathematik bis zu moderner Materialwissenschaft - der Dodekaederstumpf bleibt ein zeitloses Symbol für die Verbindung zwischen mathematischer Theorie und praktischer Anwendung. Seine perfekte Balance aus Komplexität und Harmonie macht ihn zu einem der schönsten Beispiele für die Kraft geometrischer Transformation und die anhaltende Relevanz klassischer mathematischer Prinzipien in der modernen Welt.

Abgeschrägtes Dodekaeder • Abgeschrägtes Hexaeder • Dodekaederstumpf • Hexaederstumpf • Ikosidodekaeder • Ikosaederstumpf • Ikosidodekaederstumpf • Kuboktaeder • Kuboktaederstumpf • Oktaederstumpf • Rhombenikosidodekaeder • Rhombenkuboktaeder • Tetraederstumpf