Rhombenkuboktaeder berechnen

Rechner und Formeln zur Berechnung eines Rhombenkuboktaeder

Rhombenkuboktaeder Rechner

Der Rhombenkuboktaeder

Ein Rhombenkuboktaeder ist ein halbregelmäßiger Körper aus 8 gleichseitigen Dreiecken und 18 Quadraten.

Bekannten Parameter eingeben
Welcher Parameter ist bekannt?
Wert des ausgewählten Parameters
Rhombenkuboktaeder-Eigenschaften

Archimedischer Körper: Halbregelmäßiger konvexer Polyeder

26 Flächen 48 Kanten 24 Ecken 8 Dreiecke + 18 Quadrate
Rhombenkuboktaeder-Berechnungsergebnisse
Seitenlänge a:
Volumen V:
Oberfläche S:
Umkugelradius rc:
Kantenradius rm:

Rhombenkuboktaeder-Struktur

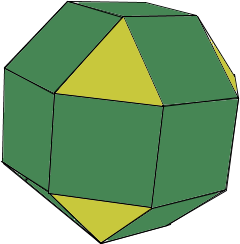
Rhombenkuboktaeder

Ein Rhombenkuboktaeder ist ein Archimedischer Körper.
Er besteht aus 8 gleichseitigen Dreiecken und 18 Quadraten.


Was ist ein Rhombenkuboktaeder?

Ein Rhombenkuboktaeder ist einer der dreizehn Archimedischen Körper:

  • Definition: Halbregelmäßiger konvexer Polyeder
  • Flächen: 8 gleichseitige Dreiecke + 18 Quadrate
  • Ecken: 24 identische Ecken
  • Kanten: 48 identische Kanten
  • Symmetrie: Oktaedrische Symmetriegruppe
  • Form: Regelmäßiges Achteck bei Betrachtung senkrecht zu einem Quadrat

Geometrische Eigenschaften des Rhombenkuboktaeder

Der Rhombenkuboktaeder besitzt faszinierende geometrische Eigenschaften:

Grundparameter
  • Seitenlänge (a): Kantenlänge aller Kanten
  • Flächen: 26 reguläre Polygone (8 Dreiecke + 18 Quadrate)
  • Euler-Charakteristik: V - E + F = 24 - 48 + 26 = 2
  • Duale Form: Deltoidal-Ikositetraeder
Besondere Eigenschaften
  • Archimedischer Körper: Alle Ecken sind kongruent
  • Vertex-Figur: (3.4.4.4) - Dreieck und drei Quadrate
  • Oktaedrische Symmetrie: 48 Symmetrieoperationen
  • Querschnitt: Regelmäßiges Achteck senkrecht zu Quadraten

Mathematische Beziehungen

Der Rhombenkuboktaeder folgt präzisen mathematischen Gesetzen:

Volumenberechnung
V = (2/3)a³(6+5√2)

Das Volumen wächst kubisch mit der Seitenlänge. Der Faktor enthält die Quadratwurzel aus 2.

Oberflächenberechnung
S = 2a²(9+√3)

Die Oberfläche berücksichtigt Dreiecks- und Quadratflächen. √3 stammt aus den gleichseitigen Dreiecken.

Anwendungen des Rhombenkuboktaeder

Rhombenkuboktaeder finden Anwendung in verschiedenen Bereichen:

Kristallographie & Chemie
  • Kristallstrukturen und Molekülgeometrie
  • Fullerene und Käfigverbindungen
  • Packungsstrukturen in Festkörpern
  • Koordinationsgeometrie in Komplexen
Architektur & Design
  • Geodätische Kuppeln und Raumstrukturen
  • Moderne skulpturale Architektur
  • Spielwürfel und Puzzle-Design
  • Dekorative Elemente und Ornamentik
Mathematik & Informatik
  • Graphentheorie und Netzwerktopologie
  • 3D-Computergrafik und Rendering
  • Optimierungsprobleme in der Geometrie
  • Symmetriegruppen und Gruppentheorie
Spiele & Bildung
  • Geometrische Puzzle und Denkspiele
  • Lehrmodelle für Stereometrie
  • Würfelspiele mit ungewöhnlicher Form
  • Virtual Reality und 3D-Visualisierung

Formeln für den Rhombenkuboktaeder

Volumen V
\[V = \frac{2 \cdot a^3 \cdot (6+5\sqrt{2})}{3}\]

Volumen in Abhängigkeit der Seitenlänge a

Oberfläche S
\[S = 2 \cdot a^2 \cdot (9+\sqrt{3})\]

Gesamtoberfläche aller 26 Flächen

Umkugelradius rc
\[r_c = \frac{a \cdot \sqrt{5+2\sqrt{2}}}{2}\]

Radius der umschreibenden Kugel

Kantenradius rm
\[r_m = \frac{a \cdot \sqrt{4+2\sqrt{2}}}{2}\]

Radius der Kugel, die alle Kanten berührt

Seitenlänge a (Umkehrformeln)
\[a = \sqrt[3]{\frac{3V}{2(6+5\sqrt{2})}}\]

aus Volumen

\[a = \sqrt{\frac{S}{2(9+\sqrt{3})}}\]

aus Oberfläche

\[a = \frac{2r_c}{\sqrt{5+2\sqrt{2}}}\]

aus Umkugelradius

\[a = \frac{2r_m}{\sqrt{4+2\sqrt{2}}}\]

aus Kantenradius

Seitenlänge aus anderen Parametern berechnen

Rechenbeispiel für einen Rhombenkuboktaeder

Gegeben
Seitenlänge a = 6

Gesucht: Alle Eigenschaften des Rhombenkuboktaeder

1. Volumenberechnung
\[V = \frac{2 \times 6^3 \times (6+5\sqrt{2})}{3}\] \[V = \frac{2 \times 216 \times 13.07}{3}\] \[V = 1879.9\]

Das Volumen beträgt etwa 1880 Kubikeinheiten

2. Oberflächenberechnung
\[S = 2 \times 6^2 \times (9+\sqrt{3})\] \[S = 2 \times 36 \times 10.73\] \[S = 772.7\]

Die Oberfläche beträgt etwa 773 Flächeneinheiten

3. Umkugelradius
\[r_c = \frac{6 \times \sqrt{5+2\sqrt{2}}}{2}\] \[r_c = \frac{6 \times 2.41}{2}\] \[r_c = 7.23\]

Umkugelradius beträgt etwa 7.23

4. Kantenradius
\[r_m = \frac{6 \times \sqrt{4+2\sqrt{2}}}{2}\] \[r_m = \frac{6 \times 2.31}{2}\] \[r_m = 6.93\]

Kantenradius beträgt etwa 6.93

5. Vollständiger Rhombenkuboktaeder
Seitenlänge a = 6.00 Volumen V = 1879.9
Oberfläche S = 772.7 Umkugelradius rc = 7.23
Kantenradius rm = 6.93

Ein perfekter Archimedischer Körper mit allen berechneten Eigenschaften

Der Rhombenkuboktaeder: Eleganz der Archimedischen Körper

Der Rhombenkuboktaeder ist einer der dreizehn Archimedischen Körper und verkörpert die elegante Symmetrie halbregelmäßiger Polyeder. Benannt nach dem antiken griechischen Mathematiker Archimedes, fasziniert dieser Körper durch seine perfekte Kombination aus gleichseitigen Dreiecken und Quadraten.

Definition und charakteristische Eigenschaften

Der Rhombenkuboktaeder zeichnet sich durch folgende Merkmale aus:

  • Archimedischer Körper: Halbregelmäßiger konvexer Polyeder mit identischen Ecken
  • Flächenstruktur: 8 gleichseitige Dreiecke und 18 Quadrate (insgesamt 26 Flächen)
  • Topologie: 24 Ecken und 48 Kanten nach der Euler'schen Polyederformel
  • Vertex-Figur: An jeder Ecke treffen sich genau ein Dreieck und drei Quadrate (3.4.4.4)
  • Oktaedrische Symmetrie: Besitzt die volle Symmetriegruppe des Oktaeders
  • Dual-Körper: Das Deltoidal-Ikositetraeder ist sein dualer Polyeder

Historische Entwicklung und mathematische Bedeutung

Antike Ursprünge

Obwohl nach Archimedes benannt, waren die Archimedischen Körper bereits den antiken Griechen bekannt. Sie entstehen durch systematische Abschrägung der platonischen Körper.

Renaissance-Wiederentdeckung

Johannes Kepler und andere Renaissance-Mathematiker studierte diese Körper intensiv und erkannten ihre Bedeutung für Kristallographie und Astronomie.

Moderne Anwendungen

Heute findet der Rhombenkuboktaeder Anwendung in Materialwissenschaft, Architektur, Computergrafik und als Modell für komplexe molekulare Strukturen.

Gruppensymmetrie

Die Symmetriegruppe des Rhombenkuboktaeder ist isomorph zur oktaedrischen Gruppe Oh mit 48 Symmetrieoperationen.

Konstruktion und geometrische Verwandtschaften

Der Rhombenkuboktaeder kann auf verschiedene Weise konstruiert werden:

Konstruktion durch Abschrägung

Entsteht durch gleichmäßige Abschrägung aller Kanten eines Würfels oder Oktaeders. Dabei werden die ursprünglichen Flächen zu kleineren Quadraten, während neue dreieckige Flächen entstehen.

Koordinatengeometrie

Die Eckpunkte können systematisch in einem kartesischen Koordinatensystem durch Permutationen von (±1, ±1, ±(1+√2)) dargestellt werden.

Verwandte Polyeder

Steht in enger Beziehung zum Kuboktaeder und zum abgeschrägten Hexaeder (Kuboktaederstumpf). Diese Körper bilden eine Familie verwandter Archimedischer Polyeder.

Platonische Verbindungen

Entsteht aus Würfel und Oktaeder durch kontinuierliche Deformation. Repräsentiert einen "Mittelweg" zwischen diesen beiden dualen platonischen Körpern.

Wissenschaftliche und technische Anwendungen

Die Bedeutung des Rhombenkuboktaeder erstreckt sich über reine Mathematik:

  • Kristallographie: Modell für komplexe Kristallstrukturen und Gitterdefekte
  • Molekularchemie: Geometrie großer Käfigmoleküle und Fullerene
  • Architektur: Geodätische Strukturen und moderne Kuppelbauten
  • 3D-Computergrafik: Effiziente Darstellung komplexer 3D-Objekte
  • Spieltheorie: Ungewöhnliche Würfelformen für Strategiespiele
  • Optimierung: Packungsprobleme und Raumaufteilung
  • Nanotechnologie: Design nanostrukturierter Materialien

Besondere mathematische Eigenschaften

Numerische Konstanten

Die Formeln enthalten elegante Ausdrücke mit √2 und √3, was die tiefe Verbindung zu quadratischen und hexagonalen Strukturen widerspiegelt.

Isoperimetrische Eigenschaften

Unter allen Polyedern mit 26 Flächen besitzt der Rhombenkuboktaeder besondere Optimalitätseigenschaften bezüglich Oberfläche-Volumen-Verhältnis.

Dualität

Das Deltoidal-Ikositetraeder als dualer Körper zeigt die elegante Beziehung zwischen Ecken und Flächen in der Polyedergeometrie.

Symmetrieerhaltung

Trotz der Mischung verschiedener Flächentypen bleibt die hohe oktaedrische Symmetrie vollständig erhalten - ein Zeichen geometrischer Perfektion.

Zusammenfassung

Der Rhombenkuboktaeder verkörpert die mathematische Eleganz der Archimedischen Körper in vollendeter Form. Seine harmonische Verbindung von Dreiecken und Quadraten, gepaart mit oktaedrischer Symmetrie, macht ihn zu einem faszinierenden Studienobjekt der Geometrie. Von der antiken griechischen Mathematik bis zur modernen Nanotechnologie inspiriert dieser Polyeder Wissenschaftler und Ingenieure. Seine mathematischen Eigenschaften - von den eleganten Formeln mit irrationalen Konstanten bis zur komplexen Symmetriestruktur - zeigen die tiefe Schönheit geometrischer Ordnung. Als Brücke zwischen den platonischen Körpern und komplexeren polyedrischen Strukturen repräsentiert der Rhombenkuboktaeder das Gleichgewicht zwischen Einfachheit und Komplexität, das die Mathematik so faszinierend macht.

Abgeschrägtes Dodekaeder • Abgeschrägtes Hexaeder • Dodekaederstumpf • Hexaederstumpf • Ikosidodekaeder • Ikosaederstumpf • Ikosidodekaederstumpf • Kuboktaeder • Kuboktaederstumpf • Oktaederstumpf • Rhombenikosidodekaeder • Rhombenkuboktaeder • Tetraederstumpf